[ 오늘 배운 내용 ]
1. matplotlib
2. CRISP-DM 데이터 분석 방법론 (EDA & CDA)
3. 단변량 분석 - 숫자형 변수
- 기초통계량 분석 : mean, mode, 4분위수
- 그래프 : 히스토그램, 밀도함수 그래프 (KDE plot), 박스플롯
4. 단변량 분석 - 범주형 변수
- 기초통계량 분석 : 범주별 빈도수, 범주별 비율
- 그래프 : barplot, piechart
지난 데이터 분석 시간에 조금 배워보았던 matplotlib을 제대로 사용해서 많은 그래프를 그려보았고, CRISP-DM 모델의 그림을 보며 각 절차의 세부내용을 배웠다.
그다음 CRISP-DM의 데이터 이해 단계의 EDA 단계와 CDA 단계 중 EDA 단계의 단변량 분석을 직접 코드를 실행해가며 연습해보았다.
숫자형과 범주형 변수에 대해 각각 기초통계량을 분석해보고 그래프를 그려보았다.
수많은 양의 데이터를 한 눈에 파악하는 방법은 그래프와 통계량 두 가지가 있다.
오늘 수업에서는 이 두 가지 내용을 다양하게 코드로 구현해보았다.
[ Matplotlib ]
데이터 시각화는 단순히 보기 좋은 그래프를 그리거나 통계적으로 하는 것 외에도 비즈니스의 인사이트를 파악해야 하는 것이 목적이 되어야 한다.
matplotlib.pyplot
파이썬에서 그래프를 그릴 때 기본이 되는 라이브러리
데이터 분석을 위한 다양한 차트들을 제공
- 그래프 그리기
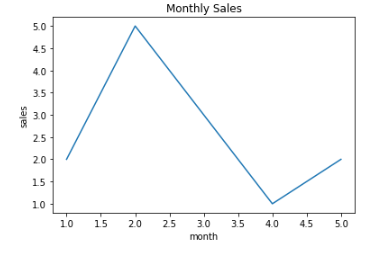
dict1 = {'v1': [1,2,3,4,5], 'v2': [2,5,3,1,2]}
plt.plot('v1', 'v2', data = dict1)
plt.xlabel('month') # x축 이름 표시
plt.ylabel('sales') # y축 이름 표시
plt.title('Monthly Sales') # 그래프 제목 표시
plt.show()- plt.plot( x축, y축, data=사용데이터 ) : 기본적인 라인차트 그래프를 그려준다.
- plt.show() : 위에서 만든 그래프를 화면에 보여준다. (주피터노트북 환경에서는 자동으로 보여주지만 안되는 환경도 있으므로 습관적으로 코드를 밑에 적어주자)
- 그래프에 라인 스타일 적용
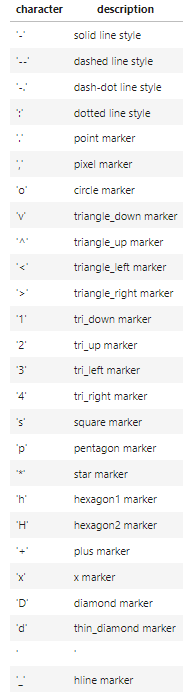
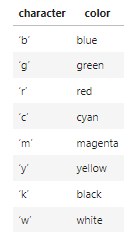
plt.plot() 실행 시 라인의 스타일을 조정할 수 있다. '[ color ][ marker ][ linestyle ]'의 형식으로 지정해주며 순서는 상관없다.
각 스타일의 옵션이 정리된 표는 아래와 같다.
아래 코드는 위에서 그린 그래프에 라인 스타일 옵션을 지정해주었다. go--에서 g는 초록색, o는 동그라미 마커, --는 점선을 나타낸다.
dict1 = {'v1': [1,2,3,4,5], 'v2': [2,5,3,1,2]}
plt.plot('v1', 'v2', 'go--', data = dict1)
plt.xlabel('month')
plt.ylabel('sales')
plt.title('Monthly Sales')
plt.show()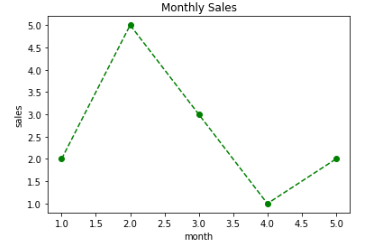
- 여러 그래프 겹쳐서 그리기
한 프레임 안에 여러 그래프를 같이 그려서 비교해야 하는 경우가 많이 필요할 것이다.
이때는 그냥 plt.plot()을 두번 해주면 된다.
dict1 = {'v1': [1,2,3,4,5], 'v2': [2,5,3,1,2], 'v3':[4,6,7,6,5]}
plt.plot('v1', 'v2', 'go--', data = dict1, label = 'apple')
plt.plot('v1', 'v3', 'rs-', data = dict1, label = 'mango')
plt.xlabel('month')
plt.ylabel('sales')
plt.title('Monthly Sales')
plt.legend()
plt.grid()
plt.show()각 그래프의 스타일을 다르게 해주었고, plot() 안에 label 옵션으로 각 그래프의 이름을 표시해 줄 수 있다. 지정해준 label은 아래의 plt.legend()를 실행해주어야 화면에 나타나고, plt.grid()로 그리드도 넣어줄 수 있다.
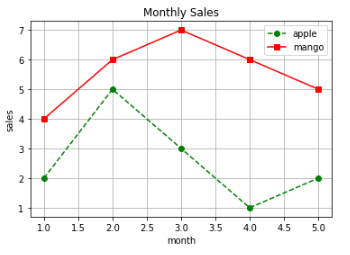
그 밖에
- plt.xlim( 시작, 끝 ) : x축 범위 지정
- plt.ylim( 시작, 끝 ) : y축 범위 지정
- plt.figure( figsize = ( 가로, 세로 ) ) : 그래프 크기 조정 (디폴트는 6.4, 4.4)
- plt.axhline( y좌표값, color, linestyle ) : 수평선 추가
- plt.axvline( x좌표값, color, linestyle ) : 수직선 추가
- plt.text( x좌표, y좌표, '추가할텍스트' ) : 그래프에 텍스트 추가
- 여러 그래프 나눠서 그리기
한번에 여러 그래프를 각각 그려줄 때에는 plt.subplot( rows, cols, index )을 사용해준다.
rows와 cols로 그래프들의 전체 프레임을 잡아주고 index로 몇번째 그래프인지를 표시한다.
ex1)
- subplot( 2, 1, 1) : 2행 1열 중 1번째
- subplot( 2, 1, 2) : 2행 1열 중 2번째
| subplot( 2, 1, 1) |
| subplot( 2, 1, 1) |
ex2)
- subplot( 2, 2, 1) : 2행 2열중 1번째
- subplot( 2, 2, 2) : 2행 2열중 2번째
- subplot( 2, 2, 3) : 2행 2열중 3번째
- subplot( 2, 2, 4) : 2행 2열중 4번째
| subplot( 2, 2, 1) | subplot( 2, 2, 2) |
| subplot( 2, 2, 3) | subplot( 2, 2, 4) |
dict1 = {'v1': [1,2,3,4,5], 'v2': [2,5,3,1,2], 'v3':[4,6,7,6,5]}
plt.subplot(2,1,1)
plt.plot('v1', 'v2', 'go--', data = dict1)
plt.show()
plt.subplot(2,1,2)
plt.plot('v1', 'v3', 'rs-', data = dict1)
plt.show()
plt.tight_layout() # 그래프간 간격을 적절히 맞추기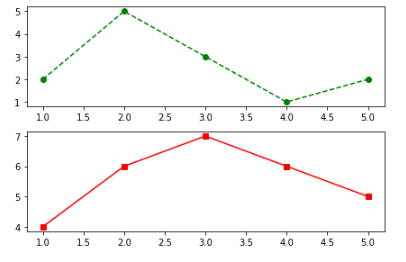
subplot의 밑에 그릴 그래프의 코드를 적어주고 다음 subplot의 밑에 다음 그래프의 코드를 적어주면 된다.
데이터 분석 방법론 : CRISP-DM
아래 그림은 매 수업마다 보는 것 같다.
오늘 수업에서는 2번째 과정에 해당하는 Data Understanding에 관련되는 내용이 많았다.
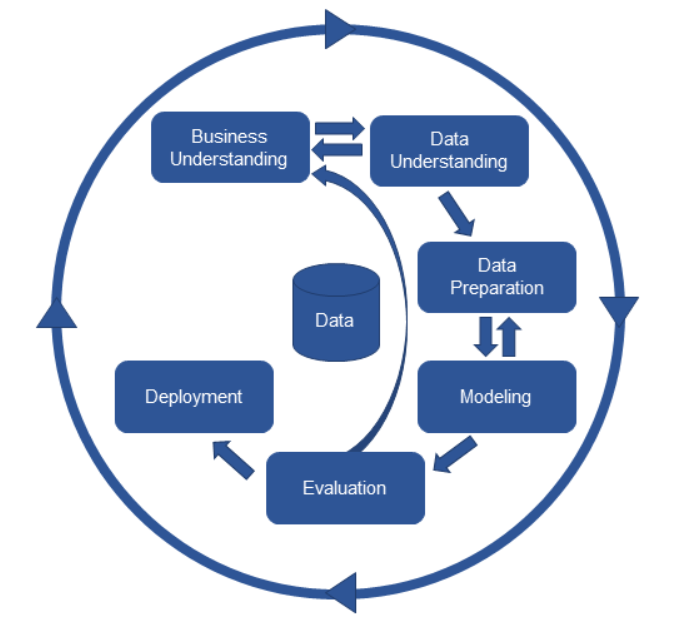
1. Business Understanding (비즈니스 이해)
- 비즈니스 문제 정의
- 데이터 분석 방향 및 목표 수립
- 초기 가설 수립 (X -> Y : Y에 영향을 주는 요인 X는 무엇인가? 를 알아내는 과정)
2. Data Understanding (데이터 이해)
- 데이터 원본 식별 및 취득
- 가용 데이터 수집 (하나의 데이터프레임으로)
- 데이터 탐색 : EDA, CDA
- 전처리 전략 수립
3. Data Preparation (데이터 준비)
- 추가변수 도출
- 결측치(NaN값) 조치
- 가변수화 (Dummy variables)
- 스케일링 (Scaling)
- 데이터 분할 (target-feature, test-train-validation)
4. Modeling (모델링)
- 중요 변수 선정
- 모델 생성
- 모델 성능 검증
5. Evaluation (평가)
- 모델에 대한 최종평가 : Test Set 이용 (기술적 관점)
- 비즈니스 기대가치 평가 (비즈니스적 관점)
6. Deployment (배포)
EDA & CDA
데이터 이해 단계에서 데이터를 탐색하는 과정의 두 가지 방법으로, 비즈니스 이해 단계에서 세운 X->Y에 대한 가설이 맞는지에 대한 검증을 하는 과정이다.
데이터를 시각화 하고, 데이터의 통계량을 같이 비교해보며 검증한다.
Exploratory Data Analysis : 탐색적 데이터 분석
비즈니스와 해결해야 할 문제를 더 잘 이해하기 위해 데이터에 대해 차트와 기초통계량을 이용하여 분포를 파악한다.
--> 데이터를 시각화, 수치화 방법을 통해 더 잘 파악하는 과정
Confirmatory Data Analysis : 확증적 데이터 분석
가설에 대해 검증하고 (데이터가 관련이 있는지) 필요시 실험을 통해 확인한다.
--> 시각화, 수치화 방법으로 파악한 데이터에 대해서 관련이 있는지 가설에 대해 검증하고, 필요시 실험을 통해서도 확인하는 과정
일반적으로 탐색적 데이터 분석 과정이 진행되는 순서는 다음과 같다.
- 개별 변수(feature, target)의 분포를 살펴본다.
- feature와 target 같의 관계를 살펴본다. (가설 검증)
- feature들 간의 관계를 살펴본다.
먼저 개별 변수를 분석하는 단변량 분석을 숫자형과 범주형 변수에 대해 수행해보았다.
숫자형과 범주형 변수별로, 기초통계량(수치화)과 그래프(시각화)를 확인해주는 도구들은 다음과 같다.
| 기초통계량 | 그래프 | |
| 숫자형 | mean() mode() 4분위수 등 |
히스토그램 (Histogram) 밀도함수 그래프 (Density plot) 박스플롯 (Box plot) |
| 범주형 | 범주별 빈도수 범주별 비율 |
Bar plot Pie chart |
[ 단변량 분석 - 숫자형 데이터의 기초통계량 (대푯값) ]
숫자형 데이터를 기초통계량으로 수치화하여 분석할 때는 평균, 중위수, 최대최소값, 최빈값, 4분위수, 표준편차 등을 구해주면 된다. 판다스의 데이터프레임 자료형은 이런 기초통계량들을 쉽게 구할 수 있는 다양한 메소드들이 존재한다.
평균 (mean)
- 산술평균 : 일반적인 평균
- 조화평균 : 두 수의 역수에 대한 평균
중위수 (median)
: 자료의 순서상 가운데 위치한 값
최빈값 (mode)
: 자료 중에서 가장 빈번하게 나타나는 값
4분위수
: 데이터의 분포를 4등분하여 각각 0% 25% 50% 75% 100%에 해당하는 부분

데이터프레임에서는 .describe()를 사용하여 기초 통계량을 한꺼번에 확인 가능하다.
데이터프레임에서 이런 기초통계량을 확인할 때 NaN값은 제외하고 확인해주어야 한다. 4분위수를 확인하는 np.percentile의 경우에는 NaN 값이 포함되어 있으면 결과를 전부 NaN값으로 보여주기 때문에 NaN값을 제외할 필요가 있다.
데이터프레임에서 NaN이 아닌 값들만 따로 뽑아올 수가 있는데 df.notnull()을 사용하면 된다.
# titanic의 Age에 대해서 각종 기초통계량 확인
# 평균
print(titanic['Age'].mean())
# 29.69911764705882
# 최빈값
print(titanic['Age'].mode())
# 0 24.0
# dtype: float64
# 중앙값
print(titanic['Age'].median())
# 28.0
# 4분위수
print(np.percentile(titanic['Age'], [0, 25, 50, 75, 100]))
# [nan nan nan nan nan]
# 4분위수 NaN 빼고 나머지 데이터 갖고오기
temp = titanic.loc[titanic['Age'].notnull(), 'Age']
print(np.percentile(temp, [0, 25, 50, 75, 100]))
# [ 0.42 20.125 28. 38. 80. ][ 단변량 분석 - 숫자형 데이터의 시각화 ]
숫자형 데이터를 시각화를 통하여 분석할 때에는 히스토그램(histogram), 밀도함수그래프(KDE plot), 박스플롯(Box plot)을 그려서 확인해 볼 수 있다.
1. 히스토그램 (Histogram)
숫자형 변수의 분포를 살펴보기 위한 가장 기본이 되는 그래프로, 구간별로 데이터가 얼마나 있는지 카운트해준다.
plt.hist( 1차원데이터, bins=구간개수, edgecolor='구분선색깔' )
plt.figure(figsize=(10,7))
plt.subplot(2, 2, 1)
plt.hist(titanic['Age'], bins=8, edgecolor='grey')
plt.title('bins=8')
plt.subplot(2, 2, 2)
plt.hist(titanic['Age'], bins=16, edgecolor='grey')
plt.title('bins=16')
plt.subplot(2, 2, 3)
plt.hist(titanic['Age'], bins=32, edgecolor='grey')
plt.title('bins=32')
plt.subplot(2, 2, 4)
plt.hist(titanic['Age'], bins=64, edgecolor='grey')
plt.title('bins=64')
plt.tight_layout()
plt.show()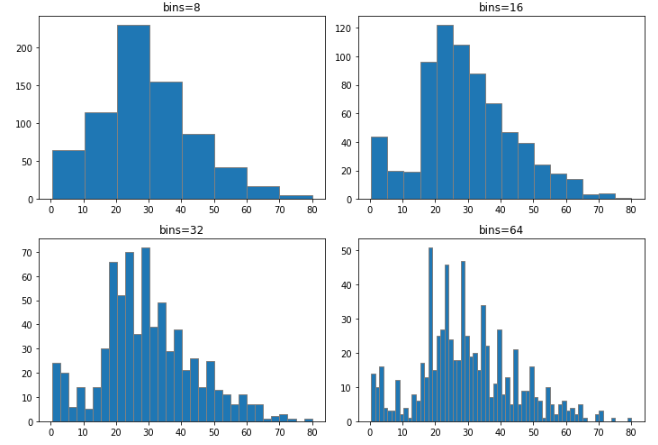
히스토그램의 구간을 어떻게 주는지에 따라 다른 그래프가 나오기 때문에 구간(bins)을 적절하게 조절해가면서 목적에 맞는 데이터의 분포를 파악해야 한다.
2. 밀도함수 그래프 (KDE plot)
히스토그램 사용시에는 구간 bins의 너비를 어떻게 잡는지에 따라 전혀 다른 모양이 될 수 있다는 단점이 있기 때문에
모든 점에서의 데이터의 밀도를 추정하는 커널 밀도 추정(KDE) 방식을 사용하여 이러한 단점을 해결한 그래프이다.
밀도함수 그래프는 matplotlib에서 제공하는 함수가 따로 없기 때문에 seaborn 라이브러리를 사용하여 그려준다.
sns.kdeplot( 1차원데이터(시리즈) )
sns.kdeplot(titanic['Fare'])
plt.show()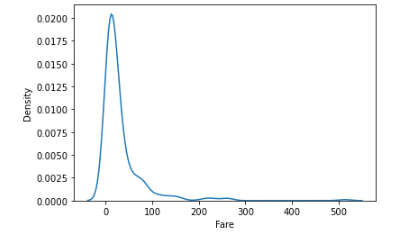
밀도함수 그래프 아래의 총 면적은 항상 1이기 때문에 측정 구간에 해당할 확률에 대한 확률 추정의 목적으로도 사용이 가능하다.
위의 그래프의 경우 타이타닉 승객의 Fare(운임) 데이터인데 0보다 작은 분포가 있는 것을 볼 수 있다. 운임이 음의 값으로 나오는 것이 말이 안된다고 생각될 것이다. 이는 밀도함수 그래프 사용 시에는 없는 값의 구간이라 해도 확률추정을 위해 스무스한 그래프가 그려지기 때문에 저렇게 보이는 것이고, 실제로 저 구간에 데이터가 분포한다는 뜻은 아니다.
3. 박스플롯 (Boxplot)
숫자들의 분포를 간단히 살펴볼 수 있게 해주는 그래프이며
plt.boxplot( 데이터, vert= ) 로 사용한다.
vert=False를 지정해주면 가로로 박스플롯을 그려주고, 디폴트는 세로로 그려준다.
# boxplot 기본
age = [19,20,23,46,21,25,26,25,28,31,37,24,28,34,38,33,32,29,27,24]
plt.boxplot(age)
plt.show()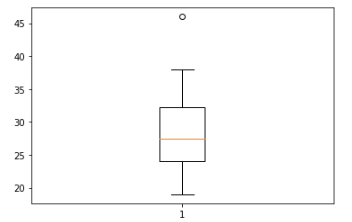
# 가로로 그리기
age = [19,20,23,46,21,25,26,25,28,31,37,24,28,34,38,33,32,29,27,24]
plt.boxplot(age, vert = False)
plt.show()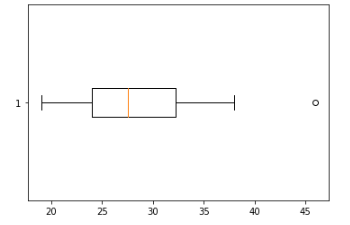
가로로 그린 박스플롯을 기준으로 설명하자면
박스플롯에서 가운데 박스의 왼쪽 변은 해당 데이터 분포의 1사분위수, 가운데 노란 선은 2사분위수, 오른쪽 변은 3사분위수를 나타낸다.
가장 왼쪽과 오른쪽에 있는 데이터는 최소값과 최대값을 나타내며 박스에서 양옆으로 뻗은 선의 끝부분은
IQR = 3사분위 - 1사분위 의 IQR 값을
- 왼쪽 : min과 1사분위 - (1.5 * IQR) 를 비교했을 때 큰 값
- 오른쪽 : max과 3사분위 + (1.5 * IQR) 를 비교했을 때 작은 값
으로 지정해준 것이다. 이 끝부분은 펜스라고 부르며 펜스의 바깥에 있는 데이터들은 Outlier(이상치)인지 판단해 볼 필요가 있다고 생각해 볼 수가 있다.
방금 소개한 3가지 그래프들을 봤을 때 데이터의 분포 상황을 빠르게 파악할 수 있을 필요가 있다.
[ 단변량 분석 - 범주형 데이터의 기초통계량]
범주형 데이터의 경우에는 숫자형 데이터처럼 각각의 값을 구하는 것보다 범주별 빈도수와 범주별 비율을 구해 주는 것이 카테고리로 나누는 범주형 데이터의 특성에 더 부합한다.
범주형 데이터에서는 판다스의 .value_counts() 메서드를 활용하여 해당 범주형 변수의 각각의 값 별 개수를 파악하고, 이를 활용해서 범주별 비율을 구해 기초통계량을 파악할 수 있다.
NaN값이 포함된 비율과 NaN값이 포함되지 않은 비율을 모두 구할 수 있는데 이를 위해 NaN값을 먼저 확인해준다.
titanic.isna().sum()
# PassengerId 0
# Survived 0
# Pclass 0
# Name 0
# Sex 0
# Age 177
# Fare 0
# Embarked 2
# dtype: int64titanic.shape
# (891, 8)
print(titanic['Embarked'].value_counts())
print('-'*50)
print(titanic['Embarked'].value_counts()/titanic.shape[0]) # NaN 포함된 건수 비율
print('-'*50)
print(titanic['Embarked'].value_counts()/titanic['Embarked'].count()) # count() ==> NaN을 빼고 카운트 해줌
# Southhampton 644
# Cherbourg 168
# Queenstown 77
# Name: Embarked, dtype: int64
# --------------------------------------------------
# Southhampton 0.722783
# Cherbourg 0.188552
# Queenstown 0.086420
# Name: Embarked, dtype: float64
# --------------------------------------------------
# Southhampton 0.724409
# Cherbourg 0.188976
# Queenstown 0.086614
# Name: Embarked, dtype: float64
value_counts로 구한 범주형 변수의 각 범주값의 개수에 해당 범주형 변수 데이터의 전체개수를 나눠주어서 비율을 파악할 수가 있다.
NaN값을 제외한 데이터의 개수는 count() 메서드로 구할 수 있다.
[ 단변량 분석 - 범주형 데이터의 시각화 ]
범주형 데이터의 시각화 시에는 bar chart와 pie chart를 사용할 수 있다. 해당 차트들은 범주형 데이터의 각 범주값 별 비율을 파악하기 좋다.
1. Bar chart
범주형 데이터의 각 범주값의 수를 센 것을 시각화하여 막대그래프의 형식으로 보여주는 도구이다.
bar chart를 그릴 때에는 범주 이름과 값이 필요하므로, 집계작업이 선행되어야 한다.
bar chart를 그리는 방법은 두가지가 있는데, 그냥 pyplot으로 그릴 수 있고, seaborn을 사용해서도 그릴 수 있다.
- pyplot 사용
pyplot 사용 시에는plt.bar( 인덱스, 값 ) 의 형식으로 그릴 수 있다.
이 때, 인덱스와 값에 넣어줄 범주 이름과 값이 필요하기 때문에 집계작업이 먼저 선행되어야 한다.
temp = titanic['Pclass'].value_counts()
print(temp) # 시리즈임 --> 인덱스, 값 있음
print(temp.index)
print(temp.values)
# 3 491
# 1 216
# 2 184
# Name: Pclass, dtype: int64
# Int64Index([3, 1, 2], dtype='int64')
# [491 216 184]집계해준 값을 넣어서 그래프를 그려보았다.
plt.bar(temp.index, temp.values)
plt.show()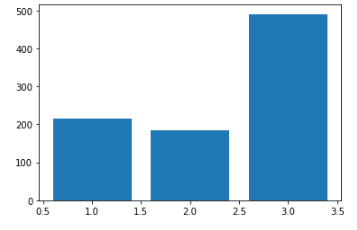
plt.barh()로 그리면 가로로 그릴 수 있다.
# 가로로 그리기
plt.barh(temp.index, temp.values)
plt.show()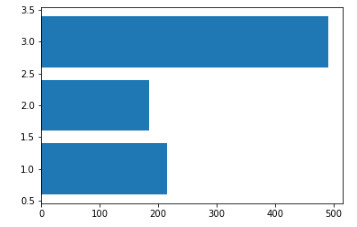
- seaborn의 countplot() 사용
seaborn 라이브러리에서 sns.countplot( 1차원데이터(시리즈) ) 을 사용하면 집계과 bar plot 그리는 것을 한꺼번에 수행할 수 있다. (pyplot 사용하는 것보다 훨씬 편한 방법 -> bar plot을 그릴 때는 seaborn을 사용하자!!)
seaborn 사용 시, x축과 y축 이름도 자동으로 붙여준다.
그리고 countplot() 안에 1차원 데이터를 y축값으로 설정해주면 bar chart를 가로로 그려준다.
# 세로로 그리기
sns.countplot(titanic['Pclass'])
plt.show()
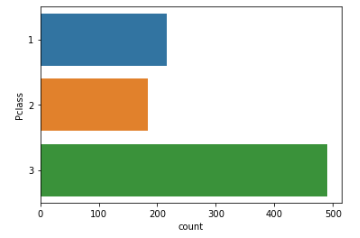
# 가로로 그리기
sns.countplot(y=titanic['Pclass'])
plt.show()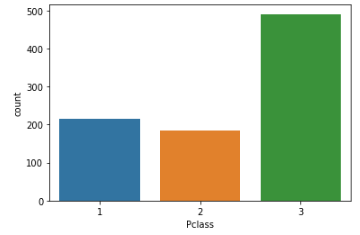
2. Pie chart
범주별 비율을 비교할 때 bar plot 말고도 파이 모양으로 데이터의 분포 비율을 확인할 수 있는 파이차트를 사용한다. bar chart와 마찬가지로 집계를 먼저 해주어야 한다.
plt.pie( 값, labels=범주이름, autopct='%.2f%%' ) 로 그려줄 수 있으며
'%.2f%%'는 소수점 아래 두번째 자리까지 퍼센트로 표시해준다는 뜻이며 원하는 형식으로 지정 가능하다.
temp = titanic['Pclass'].value_counts()
print(temp)
plt.pie(temp.values, labels = temp.index, autopct = '%.2f%%')
plt.show()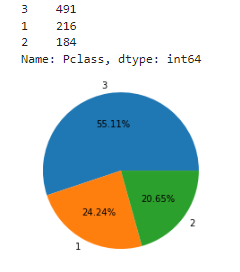
그 밖에 여러 옵션들을 넣어주어 커스터마이징이 가능하다.
- startangle=90 : 90도(12시방향)에서 시작
- counterclock=False : 시계방향으로
- explode = [0.05, 0.05,0.05] : 중심으로 부터 1,2,3 을 얼마만큼 띄울지
- shadow = True : 그림자 추가
plt.pie(temp.values, labels = temp.index, autopct = '%.2f%%',
startangle=90, counterclock=False,
explode = [0.05, 0.05, 0.05], shadow=True) # 범주 별 간격 조정 및 그림자 설정
plt.show()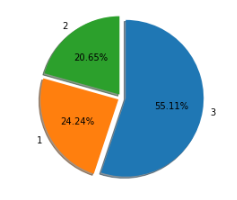
여기까지 숫자형과 범주형 개별 데이터들을 다양한 시각화와 수치화 도구들을 통해 분석해보는 단변량 분석을 수행해 보았다. 숫자를 확인하고, 그래프만 띄우고 끝내는 것이 아니라 여기서 더 나아가 데이터 처리 전략을 수립하기 위해 다음의 사항들을 확인해주는 것이 좋다.
[ 단변량 분석 시 체크사항 ]
- 값의 범위 확인
- 데이터가 모여 있는 구간(혹은 범주)과 희박한 구간(혹은 범주)를 확인
- 이상치 확인
- 결측치 확인 및 조치 방안 수립
- 가변수화, 스케일링 대상 선별
'KT AIVLE School' 카테고리의 다른 글
| (3주차 - 22.08.12) 데이터 분석 및 의미 찾기 3 - 이변량분석2 (2) | 2022.08.15 |
|---|---|
| (3주차 - 22.08.11) 데이터 분석 및 의미 찾기 2 - Seaborn,이변량분석1 (0) | 2022.08.12 |
| (3주차 - 22.08.09) 데이터 처리2 (0) | 2022.08.09 |
| (3주차 - 22.08.08) 데이터 처리1 (0) | 2022.08.08 |
| (2주차 - 22.08.05) 웹크롤링3 (0) | 2022.08.05 |
