[ 오늘 배운 내용 ]
1. 실전 단변량 분석 종합 실습
2. Seaborn 라이브러리
3. 이변량 분석 - 숫자 vs 숫자
- 시각화
- 산점도 plt.scatter()
- 수치화
- 상관분석 (상관계수, p-value)
오늘은 지난 시간에 했던 실전 단변량 분석을 카시트 판매량 데이터에 적용해서 종합적으로 실습해보는 시간을 가졌다.
그 다음 matplotlib 말고도 파이썬의 시각화 라이브러리로 많이 사용되는 seaborn 패키지를 사용하여 다양한 차트를 그려보았고, 이번에는 탐색적 데이터 분포 단계에서 feature -> target의 관계가 성립이 되는지를 살펴보는 가설 검증 과정을 위한 다변량 분석을 위한 여러 도구를 배워보았다.
Seaborn 라이브러리
matplotlib을 기반으로 다양한 색상 테마와 통계용 차트 등의 기능을 추가한 시각화 패키지이다.
matplotlib보다 더 다양하게, 더 쉽게, 더욱 다각적으로 분석할 수 있는 차트들을 제공해준다.
seaborn 라이브러리를 사용하면 아래 그림과 같은 다양한 시각화 기능을 사용할 수 있다.
- seaborn 불러오기
import seaborn as sns
- 히스토그램 (histogram)
plt.hist와 사용법은 유사한데 hue 옵션을 지정해주면 hue로 지정된 범주값별로 쪼개서 결과를 볼 수 있다.
sns.histplot(data = titanic, x='Age', bins = 16, hue = 'Survived') # hue -> 지정한 범주값별로 쪼개서 보여줌
plt.show()
- 밀도함수 그래프 (kde plot)
sns.kdeplot(data = titanic, x = 'Age', hue = 'Survived', common_norm = False)
plt.show()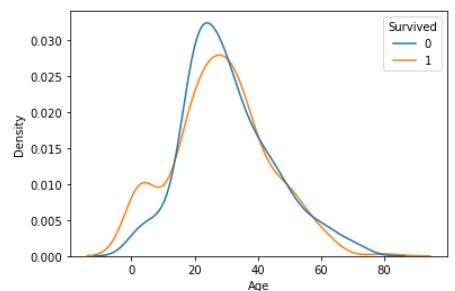
- 박스플롯 (boxplot)
박스플롯은 hue 옵션 말고 x와 y를 따로 지정해주면 범주 별로 확인이 가능하다.
sns.boxplot(data = titanic, y = 'Age', x = 'Survived') # x, y 지정해주면 범주 별 박스플롯을 보여줌
plt.show()
- sns.distplot( 데이터, bins= , hist_kws=dict() )
히스토그램과 밀도함수 그래프를 겹쳐서 표현해준다.
* hist_kws = dict() : 히스토그램을 꾸미기 위한 옵션, 딕셔너리 형태로 입력.
sns.distplot(titanic['Age'], bins = 16, hist_kws = dict(edgecolor='grey'))
plt.show()

- sns.jointplot( )
두 숫자형 변수의 분포를 한꺼번에 비교하여 보여준다.
sns.jointplot(x='Petal.Length', y='Petal.Width', data = iris, hue = 'Species')
plt.show()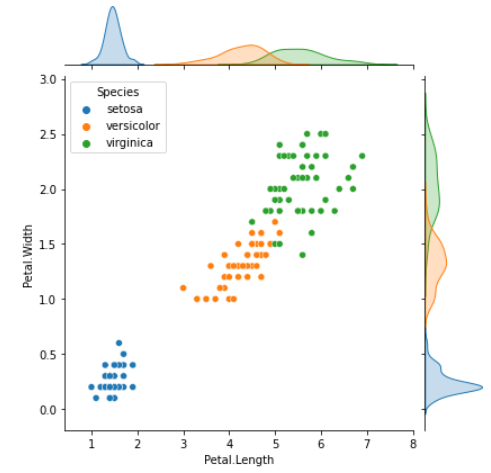
- sns.pairplot( )
모든 숫자형 변수들에 대해서 서로 비교하는 산점도를 표시해준다.
각 변수에 대해서는 히스토그램 혹은 밀도함수그래프(density plot)으로 표시해주며 시간이 오래 걸린다는 단점이 있다.
sns.pairplot(iris, hue = 'Species')
plt.show()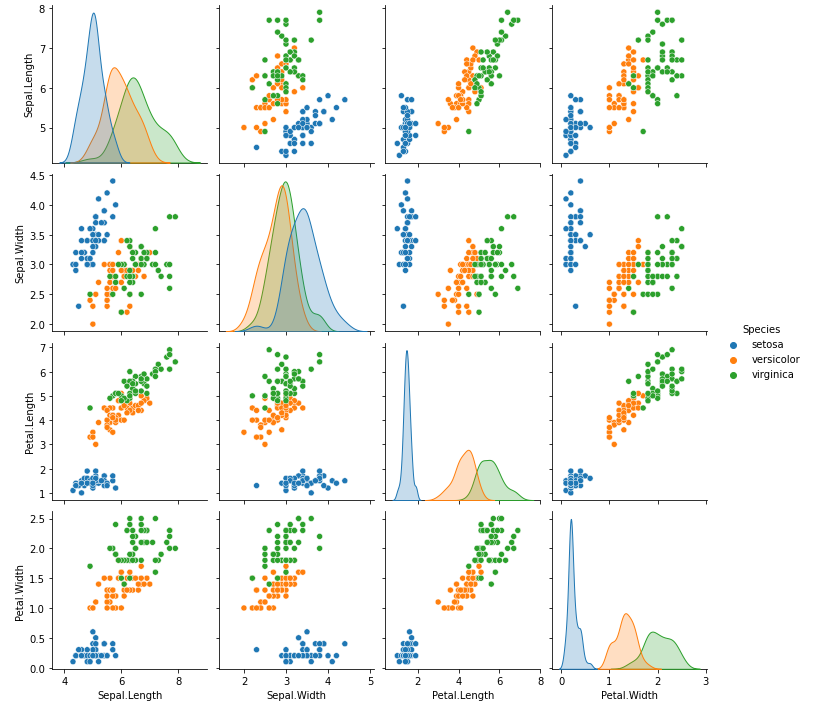
- sns.countplot( )
matplotlib에서 bar plot을 그릴 때에는 집계를 먼저 따로 해주어야 하지만 seaborn의 countplot은 집계와 barplot 그리기를 동시에 수행해준다.
sns.countplot(x="Embarked", data=titanic, hue = 'Survived')
plt.show()
- sns.barplot( ) (@@중요@@)
seaborn의 barplot은 일반적인 bar plot이 아니고, 범주별(X) 숫자(Y)의 평균을 비교하는 그래프이다.
가운데 직선은 신뢰구간을 의미한다.
신뢰구간은 간단하게 말하면 모집단의 값이 속하리라고 간주되는 값들의 범위를 만드는 것으로, 표본을 통해 모집단을 추정하기 위한 개념이다. 자세한 내용은 뒤에서 설명하도록 하겠다.
sns.barplot(x="Embarked", y="Fare", data = titanic)
plt.show()
위의 그림은 타이타닉 데이터의 승선지역(Embarked) 별 운임(Fare)의 평균을 나타낸 그래프이다. 각 막대그래프가 나타내는 값은 해당 승선지역에서의 평균 운임이고 검은색 막대기는 error bar라고 해서 신뢰구간을 나타낸다.
- sns.heatmap( )
두 범주를 집계한 결과를 색의 농도로 표현해주는 그래프이다.
집계(groupby)와 피봇(pivot)을 먼저 만들어 주어야 하며 여러 범주는 갖는 변수 비교 시에 유용하다.
* pivot : 집계된 데이터를 재구성하여 데이터프레임으로 만들어준다.
- df.pivot(index, colums, values)
# 집계
temp1 = titanic.groupby(['Embarked','Pclass'], as_index = False)['PassengerId'].count()
temp1
# EmbarkedPclass PassengerId
# 0 C 1 85
# 1 C 2 17
# 2 C 3 66
# 3 Q 1 2
# 4 Q 2 3
# 5 Q 3 72
# 6 S 1 127
# 7 S 2 164
# 8 S 3 353
# 피봇 만들기
temp2 = temp1.pivot('Embarked','Pclass', 'PassengerId')
temp2
# Pclass 1 2 3
# Embarked
# C 85 17 66
# Q 2 3 72
# S 127 164 353temp1 = titanic.groupby(['Embarked','Pclass'], as_index = False)['PassengerId'].count()
temp2 = temp1.pivot('Embarked','Pclass', 'PassengerId')
print(temp2)
# 값을 정수로, 구간 간격을 살짝 벌려서 heatmap 그리기.
sns.heatmap(temp2, annot = True, fmt = 'd', linewidth = .2)
plt.show()
이제 탐색적 데이터 분석이 진행되는 과정 중 두 변수의 관계 분석을 위해 사용되는 여러 도구들을 사용해보았다.
EDA & CDA 단계에서 어제 진행한 내용을 통해 범주형과 숫자형 개별 변수의 분포를 여러 시각화와 수치와 도구를 통해 분석해보는 시간을 가졌다.
이번 시간에는 개별 변수의 분포를 살펴본 뒤 feature와 target의 관계 즉, 내가 설정한 가설 (X -> Y)이 맞는지 확인하기 위해 두 변량간의 관계를 파악해보는 여러 도구들을 사용해보았다.
- 개별 변수(feature + target)의 분포를 살펴본다.
- feature와 target 같의 관계를 살펴본다. (가설 검증)
- feature들 간의 관계를 살펴본다.
X -> Y에서 X와 Y가 각각 숫자형과 범주형일때마다 각각 다른 시각화, 수치화 가설점증도구가 필요하다.
이를 우선 표로 크게 정리해보았다.
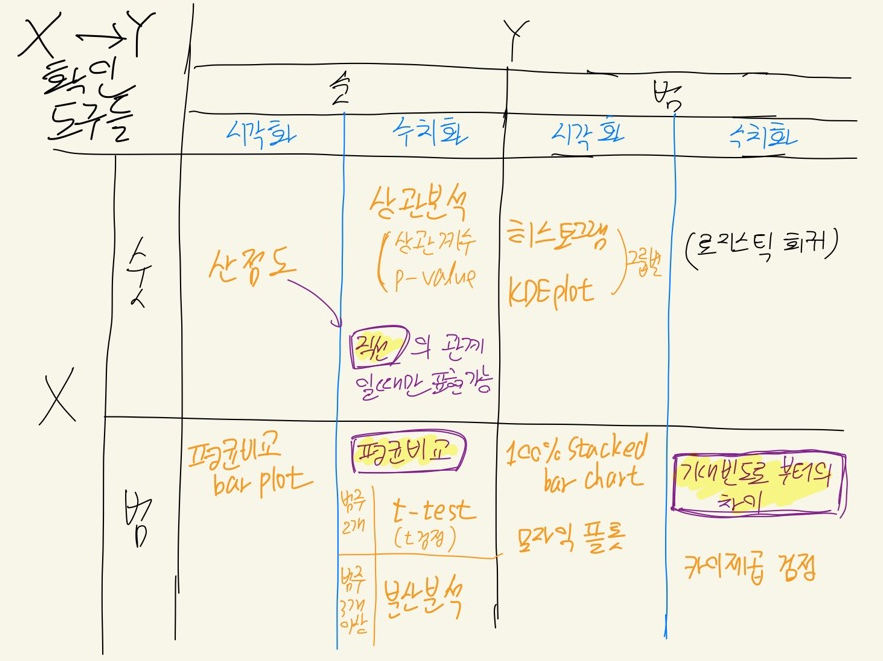
참고로 이 도구들도 모두 한계가 있다. 특히 수치화 도구는 많은 가정들이 전제되어야 하기 때문에 도구를 사용하는 데에만 집중하고 그 결과를 맹목적으로 믿어야 하는 것은 아니라는 것을 알아두자.
[ 이변량 분석 - 숫자형 -> 숫자형의 시각화 & 수치화 ]
숫자형 데이터 -> 숫자형 데이터의 가설검증을 위한 시각화 도구로는 plt.scatter() 함수를 통해 산점도를 그려보는 것이 있다.
plt.scatter( 'x변수', 'y변수', y축 값 )
plt.scatter('Temp', 'Ozone', data = air)
plt.xlabel('Temp')
plt.ylabel('Ozone')
plt.grid()
plt.show()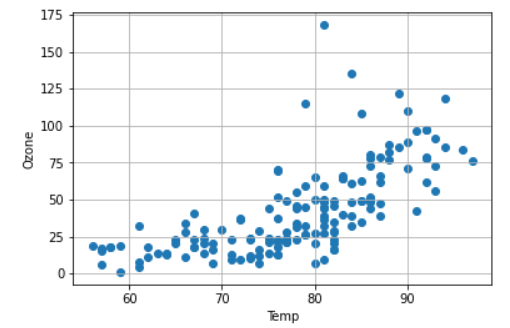
두 변수 간의 산점도 그래프를 그렸다면 이 그래프를 통해 정보를 파악할 수 있어야 한다.
plt.scatter() 말고도 sns.pairplot)=()이나 sns.jointplot()을 통해서도 다른 방식으로 산점도를 그려볼 수 있다.
위의 그래프 같은 경우는 다음과 같은 정보들을 파악할 수가 있을 것이다.
- 온도가 높을수록 오존농도가 높다.
- 80도 이후로 그래프가 좀 퍼진다.
- 80도 근처에 이상치가 많다.
숫자형X -> 숫자형Y 의 가설 검증 시에는 시각화 도구인 산점도 그리기 말고도 수치화 도구로서 상관 분석을 수행해 주어야 한다.
상관 분석은 연속형 변수 X에 대한 연속형 변수 Y의 관계를 분석할 때 사용되며 Scatter를 통해 시각화한다. (연속형=숫자형)
그려진 산점도를 통해
- 어떤 관계가 보이는지?
- 얼마나 강한 관계인지?
등의 정보를 파악하는 것이 중요한데 숫자 vs 숫자를 비교할 때 가장 중요한 관점은 바로 직선(Linearity)이다.
다음 그림은 산점도와 상관관계의 예시를 그림으로 그린 것이다.

산점도에서 두 변수 간의 관계를 파악할 때 또렷한 패턴이 보인다면 강한 관계로 볼 수 있다.
각 그림마다 상관계수 값은 -1 ~ +1 사이의 값이고, -1이면 강한 음의 상관관계, +1이면 강한 양의 상관관계이다.
상관계수를 통해 상관관계를 파악할 때에는 직선의 패턴이 관찰되는지를 확인해주는 것이 중요하다.
상관계수는 얼마나 직선으로 값들이 모여있는지를 수치화해준 값으로 절댓값 1에 가까워질 수록 직선의 형태를 강하게 띄게 된다.
위의 그림에서 봤듯이 산점도를 그려서 상관관계를 파악하기 위해서는 동시에 상관계수도 함께 비교해주어야 한다.
때문에 시각화 + 수치화는 항상 같이 해주어야 한다.
상관분석을 위해서는 scipy 패키지를 불러주어야 한다.
import scipy.stats as spst
spst.pearsonr( X,Y )의 형태로 X, Y에 대한 피어슨 상관계수를 구할 수 있다.
참고로 값에 NaN이 있으면 계산되지 않기 때문에 반드시 .notnull()로 제외하고 수행해야 합니다.
spst.pearsonr(air['Temp'], air['Ozone'])
# (0.6833717861490114, 2.197769800200274e-22)결과값은 튜플로 나오는데 (상관계수, p-value)의 형태이다.
* p-value란
귀무가설이 맞다는 전제 하에 통계값이 실제로 관측된 값 이상일 확률을 의미한다.
이는 즉 어떤 가설을 전제로 그 가설이 맞는다는 가정 하에, 내가 지금 구한 통계값이 얼마나 자주 나올 것인가를 의미하는 값이라고 이해하면 되겠다.
통계적인 용어인데 수업을 들으면서도 이해하기가 너무 힘들었다. 아래 링크에서 잘 설명이 돼있지만 사실 아직도 뭔말인지 나는 아리송하다.
일단 간단하게 정리하면 "p-value의 값이 5%보다 낮을 경우 현재 가설은 맞을 것이다." 정도로 이해하면 되겠다.
p-value란 무엇인가
p-value는, 귀무가설(null hypothesis, H0)이 맞다는 전제 하에, 통계값(statistics)이 실제로 관측된 값 이상일 확률을 의미한다. 일반적으로 p-value는 어떤 가설을 전제로, 그 가설이 맞는다는 가정 하에,
adnoctum.tistory.com
데이터프레임으로부터 바로 상관계수를 구해주는 df.corr() 메서드도 존재한다.
corr() 메서드는 NaN값을 알아서 제외하고 구해준다.
# 데이터프레임으로 부터 수치형 데이터에 대한 상관계수 구하기
air.corr() # NaN값은 제외하고 구해줌
.corr() 사용 시 모든 숫자형 변수들 상호간에 상관계수를 계산해주며, 대각선은 같은 변수끼리의 비교라서 상관계수가 1로 나온다.
따라서 대각선은 무시하고 대각선의 위쪽이나 아래쪽 둘 중 하나의 영역을 살펴보며 상관계수를 확인해주면 된다.
.corr() 사용 시 데이터프레임의 형태로 결과를 내주기 때문에 corr()의 결과로 얻은 상관계수를 heatmap으로 시각화하여 더욱 직관적으로 확인할 수도 있다.
plt.figure(figsize = (8, 8))
sns.heatmap(air.corr(), annot = True, fmt = '.3f', cmap = 'RdYlBu_r', vmin = -1, vmax = 1)
plt.show()
heatmap을 사용하면 상관계수 값을 확인 안하고도 색깔만 보고 바로 가장 높은 상관관계를 갖는 변수를 찾아낼 수 있다.
위의 예시에서는 진한 빨간색일수록 강한 양의 상관관계, 진한 파란색일수록 강한 음의 상관관계를 나타낸다.
하지만 상관계수에는 한계가 있다.
위에서 설명했다시피 상관계수는 얼마나 직선인지를 나타내는 지표이기 때문에 산점도가 직선의 패턴일 경우에만 유효한 값이 된다. 따라서 기울기는 상관이 없어지고, 직선이 아닌 다른 패턴이 명확하게 관찰되어도 상관관계는 모두 똑같이 나올 수도 있다.

위 그림의 첫번째 줄은 상관계수로 잘 설명이 가능하다.
두번째 줄을 보면 모든 경우가 직선의 형태로 관찰되며 기울기만 다르다. 하지만 상관계수는 모두 똑같은 1 아니면 -1의 값을 갖게 되어 상관계수를 통해 차이를 파악하는 것이 어렵다. 가운데 그림은 +1로 해야 하는지, -1로 해야 하는지도 모호하다.
마지막 줄의 산점도는 모두 명확한 패턴들을 갖고 있기 때문에 분명히 상관관계가 있어 보인다. 하지만 직선의 패턴이 아니기 때문에 상관계수라 0으로 나온다.
이렇게 상관계수는 직선의 관계로 표현될 때에만 사용이 가능하기 때문에 두 변수의 관계 분석 시에 상관계수만 체크하는 것이 아니라 반드시 산점도를 그려서 분포도 함께 확인해주는 것이 필요하다!!!
앞서 나왔던 p-value를 좀 더 잘 이해하기 위해 가설과 검정 이야기를 할 필요가 있다.
데이터를 사용하여 분석할 때 우리는 일부분으로 전체를 추정하고자 한다. 여기서 과거,현재,미래까지 모두 포함하는 전체 집단은 모집단, 우리가 수집한 일부분 집단을 표본 이라고 한다.
- 모집단 : 우리가 알고 싶은 대상 전체 영역(데이터)
- 표본 : 그 대상의 일부 영역(데이터)
표본으로 모집단을 추정하기 위해 모집단에 대한 가설을 수립하며, 가설은 보통 x와y의 관계를 표현한다. (x -> y)
- x에 따라 y가 차이가 있다.
- x와 y는 관계가 있다.
우리는 여기서 표본을 가지고 가설이 진짜 그러한지 검증하는데 이 과정이 가설 검증인 것이다.

먼저 귀무가설과 대립가설에 대해 알 필요가 있다.
- 귀무가설 : 반대 주장 (보수적인 입장)
- 대립가설 : 나의 주장 (새로운 가설)
용어가 헷갈릴 수도 있는데 대립가설이 바로 우리가 확인하고자 하는 새로운 가설이고, 이에 반대하는 보수적 입장의 가설이 바로 귀무가설이다.
예시를 드는 것이 이해가 빠를 것이다.
ex)
매장이 위치한 지역(x)에 따른 제품의 수요량(y)은 다를 것이다. (x -> y) : 대립가설
매장이 위치한 지역(x)과 제품의 수요량(y)은 아무런 관련이 없다. : 귀무가설
우리는 표본으로부터 대립가설을 확인하고, 모집단에서도 맞을 것이라 주장하는 것이다.
위의 예시에서 x의 값들에 따른 y가 차이가 많이 나는지를 확인해봐야 하기 때문에 x의 값에 따른 y의 차이 값의 분포를 확인해야 한다.
따라서 아래의 A매장 수요량 - B매장 수요량의 차이 분포를 보여주는 확률밀도함수를 그려보았다.
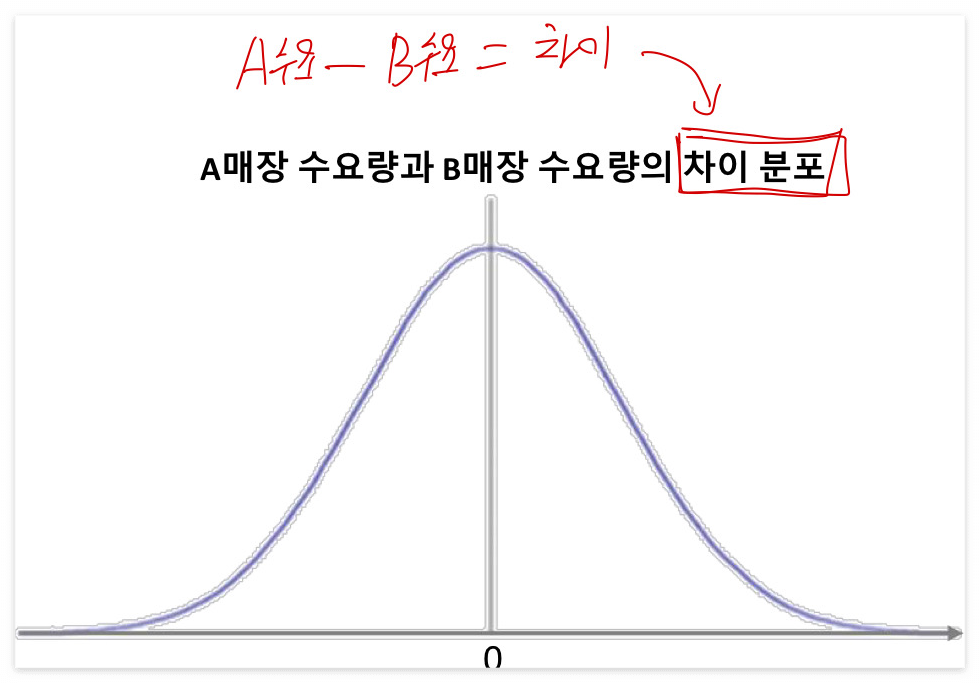
이 때 A매장과 B매장의 수요량의 차이가 커야 매장이 위치한 지역에 따라 수요량이 다르다는 것이 맞는 말이 되는 것이고 이는 즉 대립가설이 참이라는 결론으로 이어진다.
아래 그림은 확률밀도함수이기 때문에 면적은 확률을 의미하고, 0에 가까울 수록 차이가 적고 흔한 결과 / 0에서 멀어질 수록 차이가 크고 드문 결과이다.

그렇다면 A와 B 매장의 수요량의 차이가 어느 정도만큼 커야 대립가설이 참이라고 할 수 있는 것일까?
A와 B 매장 수요량의 차이가 양 끝의 노란색 칠해진 영역 정도에 위치하게 된다면 차이가 크다고 말할 수 있을 것 같다.
이러한 영역이 일반적으로 약 5%보다 작다면 차이가 크다고 한다.
이 5% 영역은 곧 대립가설이 맞다고 받아들일 때, 모집단 내에서 이 판단이 틀릴 확률이 되는 것이다.
여기서 5%는 피셔의 밀크티 실험에서 유래한 수치로 유의수준이라고 부른다.
우리는 가설검정을 수행하기 위해 참,거짓의 기준이 될 값과 비교할 검정 통계량을 계산해야 한다.
검정 통계량은 위에서 설명한 방식과 같이 일반적으로 차이의 분포를 사용해서 구하는 값들로 다음과 같은 값들이 있다.
물론 우리가 직접 구하는 것이 아닌 컴퓨터가 계산해준다.
- t 통계량
- x^2(카이제곱) 통계량
- f 통계량
검정 통계량은 기준 대비 차이로 계산되며
계산된 통계량들은 각자의 분포를 갖는다. 당연히 분포를 통해서 그 값(차이)가 큰 지, 작은 지를 판단할 수 있고, 이를 손쉽게 판단할 수 있도록 계산해 준 것이 바로 p-value이다.
여기서 p-value는 분포에서 드문 영역의 면적을 의미한다.
So,
우리는 수치화도구로 구한 값을 사용해서
대립가설이 맞다고 받아들일 때 모집단에서 틀릴 확률 (p-value = 유의확률)과 5% (유의수준)을 비교해 보고
- 5%보다 작다면 ===> 대립가설 채택
- 5%보다 크다면 ===> 귀무가설 채택
의 과정을 수행해주면 되는 것이다. (가설 검정)
'KT AIVLE School' 카테고리의 다른 글
| (4주차 - 22.08.16~22.08.19) 미니프로젝트1 (0) | 2022.08.22 |
|---|---|
| (3주차 - 22.08.12) 데이터 분석 및 의미 찾기 3 - 이변량분석2 (2) | 2022.08.15 |
| (3주차 - 22.08.10) 데이터 분석 및 의미 찾기 1 (0) | 2022.08.10 |
| (3주차 - 22.08.09) 데이터 처리2 (0) | 2022.08.09 |
| (3주차 - 22.08.08) 데이터 처리1 (0) | 2022.08.08 |

