[ 오늘 배운 내용 ]
1. 이변량 분석 - 범주 vs 숫자
- 시각화
- 평균비교
- 수치화
- 평균비교 (t-test, 분산분석)
2. 이변량 분석 - 범주 vs 범주
- 시각화
- 100% Stacked Bar chart
- Mosaic plot (모자익 플롯)
- 수치화
- x^2(카이제곱)검정
3. 이변량 분석 - 숫자 vs 범주
- 시각화
- 히스토그램, 밀도함수그래프
- 수치화
- (로지스틱 회귀)
오늘은 지난 시간에 했던 숫자형->숫자형 변수의 시각화, 수치화 도구에 이어서
범주형->숫자형, 범주형->범주형, 숫자형->범주형 변수의 여러 시각화, 수치화 도구도 다루어 보았다.
정리하기에 앞서 X->Y에서 X와Y변수의 종류에 따른 시각화, 수치화 도구들을 정리한 표를 먼저 확인해보자.
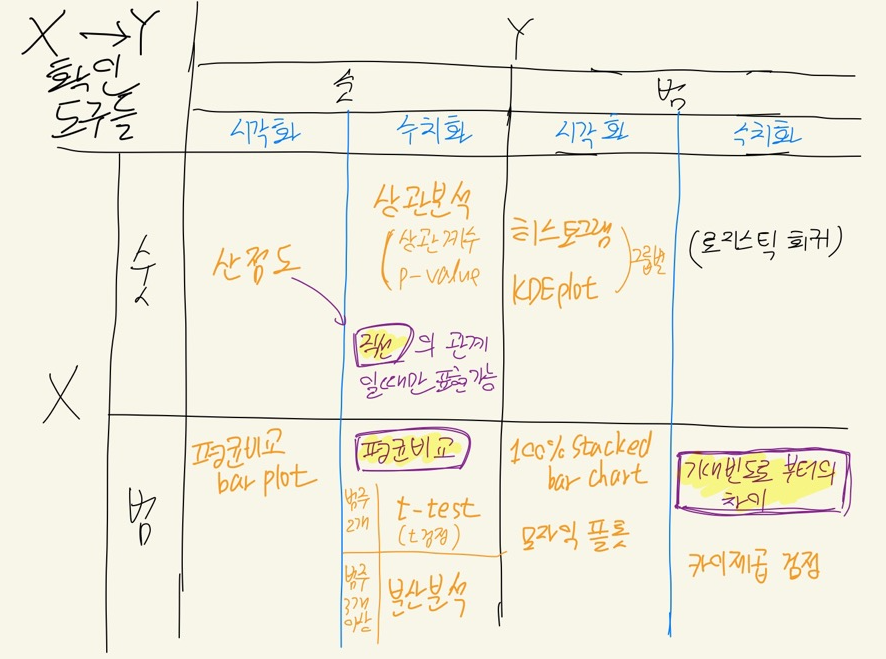
[ 이변량 분석 - 범주형 -> 숫자형의 시각화 & 수치화 ]
범주형 -> 숫자형의 관게를 살펴볼 때 가장 중요한 관점은 평균비교이다.
평균을 비교할 때는 다음의 두 가지를 고려해주어야 한다.
- 평균값이 그 집단을 대표할 수 있는가? (정규분포와 유사한 형태)
- 평균값이 믿을만 한가?
평균값이 무조건 해당 집단을 대표할 수 있는지는 무작정 판단하면 안된다.
다음과 같은 예시를 보자
임의의 한 집단을 만들어 준 뒤 이 집단의 분포를 나타내는 히스토그램을 붉은색 평균값과 함께 그려주었다.
# 임의의 한 집단 생성
pop = [round(rd.normalvariate(10, 5),1) for i in range(1000)] + [round(rd.normalvariate(38, 8),1) for i in range(750)]
mn = np.mean(pop)
print(mn)
# 21.79005714285714# 히스토그램
plt.figure(figsize=(10,6))
sns.histplot(pop, bins = 50)
plt.axvline(mn, color='r')
plt.text(mn+1, 110, "mean : {}".format(round(mn,2)), color = 'r')
plt.show()
그려진 히스토그램을 보면 붉은색의 평균값은 절대 해당 집단을 대표할 수가 없어 보인다. 평균치에 해당하는 분포는 매우 적고, 양옆으로 평균과 떨어진 지점에 많은 분포를 하고 있는 것을 볼 수 있다.
따라서 평균값이 집단을 대표할 수 있는지를 따지기 위해서 이에 대한 명확한 기준이 필요한데, 바로 분포가 정규분포의 형태를 하고 있는지를 봐주면 된다.
집단이 정규분포 형태의 분포를 갖고 있다면, 이 경우에는 평균값이 해당 집단을 대표할 수 있다.
따라서 평균값을 대표값으로 사용하기 위해서는 해당 분포가 정규분포인지를 따져볼 필요가 있다.
우리가 표본조사를 통해 모집단을 추정하 때에는 표본의 크기가 커질수록 표본의 평균(표본평균)은 모집단의 평균(모평균)에 가까워질 것이다.
평균값이 믿을만한지는 모평균과 표본평균의 오차를 통해 평가해야 하는데, 이를 확인하기 위한 지표로 표준편차와 표준오차가 있다.
표준편차란 한 집단을 설명하기 위해서 그 집단 안에서 대표값으로 평균을 구할 때, 값들이 평균값으로부터 얼마나 벗어나 있는지에 대한 이탈도를 나타내는 값이다.
표준오차란 표준편차와는 다른 개념이며 표본평균을 계산하고 나서 모평균과의 오차를 추정한 값이다.
우리가 표본을 뽑아내는 목적은 모집단을 추정하기 위함이다. 따라서 표본평균을 계산한다는 의미는 표본의 평균으로 모집단의 평균을 추정한다는 것이다. 표본의 평균을 계산하면, 표본 자체의 평균이라는 의미가 아니라, 모평균을 표본으로 추정한 평균치라는 생각을 하고 있어야 한다.
표준오차 공식은 𝑠/√𝑛 이며, s는 샘플의 표준편차, n은 데이터의 건수이다.
이 표준오차 식은 중심극한정리에 의해 나왔고, 이 표준오차로부터 우리는 신뢰구간을 계산하게 된다.
표준편차와 표준오차는 데이터프레임에서 std(), sem()으로 쉽게 구할 수 있다.
# 표준편차
titanic.groupby('Survived')['Age'].agg(['mean','std'])
# mean std
# Survived
# 0 30.626179 14.172110
# 1 28.343690 14.950952
# 표준오차
titanic.groupby('Survived')['Age'].agg(['mean','std','sem'])
# mean std sem
# Survived
# 0 30.626179 14.172110 0.688258
# 1 28.343690 14.950952 0.877950
우리는 95%의 신뢰구간의 의미에 대해서 간단하게 알고 가자
모집단에서 표본을 샘플링 후, 평균을 구하는 시도를 여러 번 수행하고 평균들을 얻게 되면 놀랍게도 이 평균들의 분포(표집분포)는 정규분포가 된다. 이는 중심극한정리에 의한 것이며 표본의 크기가 클수록 더더욱 정규분포에 가까운 형태가 된다.
따라서 95% 신뢰구간의 정확한 의미는 모집단의 값이 속하리라고 간주되는 값들의 범위를 만드는 것이다.
예를 들자면 표본을 100번 추출한다고 할 때, 일반적으로 95회 정도는 각 샘플로부터 구한 신뢰구간이 모집단의 모평균을 포함한다는 뜻이다.
아래 그래프는 수업시간에 임의의 모집단을 생성하고, 100번의 샘플링을 하여 각 표본의 평균과 신뢰구간을 빨간색 모평균과 비교해 본 결과이다.

실제로 여러번 반복해봐도 일반적으로 5-6번을 제외한 나머지 경우에는 항상 모평균이 신뢰구간에 포함되었다.
본격적으로 범주형 -> 범주형 변수의 시각화와 수치화 도구를 알아보자
시각화 도구로는 평균 비교 barplot이 있으며 seaborn 라이브러리의 sns.barplot()으로 평균과 신뢰구간을 함께 시각화할 수 있다.
수치화 도구는 2가지 경우에 따라 달라진다.
- 범주가 2개 : t-검정 (t-test)
- 범주가 3개 이상 : 분산분석 (anova)
타이타닉 데이터의 생존 여부에 따른 나이를 sns.barplot()으로 평균비교해보았다.
# 평균비교 시각화
sns.barplot(x="Survived", y="Age", data=titanic)
plt.grid()
plt.show()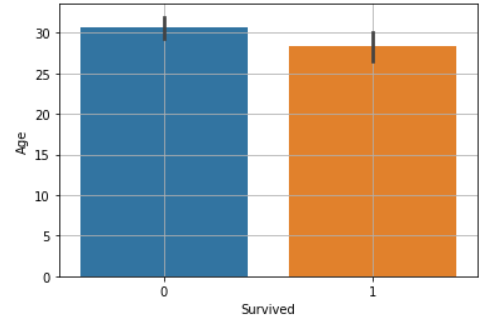
Survived 0과 1 두 범주 간에 Age의 값에 차이가 있는지를 확인하려면 평균이 다른지와 신뢰구간이 겹치지 않는지를 봐주면 된다.
시각화로 완전한 판단이 애매하니 수치화 도구도 함께 사용해 보았다.
Survived의 범주값은 0과 1 두 개 뿐이므로 t-test를 수행한다.
t-test에도 여러 종류가 있는 것 같지만 우리가 수업시간에 다룬 것은 2 sample t test 와 양측검정이다.
- 2 sample t test : 두 집단의 평균을 비교
- 양측검정 : 차이가 있냐? 없냐? 를 비교
정도로만 간단히 이해하고 넘어가자
t-test로 구하는 t통계량은 두 평균의 차이를 표준오차로 나눈 값이다. 기본적으로는 두 평균의 차이로 이해해도 좋다.
우리의 대립가설은 차이가 있다는 것을 주장하고 있으므로, t값의 절댓값이 큰지를 확인해주면 된다.
t통계량 값은 보통 -2보다 작거나, 2보다 클 때 차이가 있다고 본다.
생존여부에 따른 나이의 t통계량 값을 구해보자
NaN값은 제외해주고, 생존자와 사망자의 나이를 나눠주었다.
# 먼저 NaN이 있는지 확인
titanic.isna().sum()
# PassengerId 0
# Survived 0
# Pclass 0
# Name 0
# Sex 0
# Age 177
# SibSp 0
# Parch 0
# Ticket 0
# Fare 0
# Cabin 687
# Embarked 2
# dtype: int64
temp = titanic.loc[titanic['Age'].notnull()] # NaN이 아닌것들만
died = temp.loc[temp['Survived']==0, 'Age'] # 사망자의 나이
survived = temp.loc[temp['Survived']==1, 'Age'] # 생존자의 나이
t통계량 값은 spst.ttest_ind( B, A, equal_var=False )로 구할 수 있으며
- A와 비교할 때 B의 평균이 큰가?
- equal_var : A와 B의 분산이 같은가? 모르면 False
를 의미한다.
spst.ttest_ind(died, survived) # t통계량, p-value
# Ttest_indResult(statistic=2.06668694625381, pvalue=0.03912465401348249)결과값으로 t통계량과 p-value를 리턴해준다.
결과를 분석해보면 t통계량은 2 정도로 차이가 없진 않다고 볼 수 있으며,
p-value는 0.039 정도로 유의수준 0.05(5%) 보다 작다.
따라서 생존여부에 따른 나이는 어느 정도 관계가 있다고 분석해 볼 수 있다.
좀 더 확실한 경우의 분석을 해보기 위해 타이타닉 데이터의 성별에 따른 운임을 시각화, 수치화 해보았다.
# Sex --> Fare 시각화
sns.barplot(x='Sex', y='Fare', data=titanic)
plt.grid()
plt.show()
시각화 결과로 평균비교를 해보면 성별에 따른 운임은 평균도 차이가 큰데 신뢰구간도 전혀 겹치지 않는 것을 알 수 있다.
수치화까지 진행해보자
# Sex --> Fare 수치화
male = titanic.loc[titanic['Sex']=='male', 'Fare']
female = titanic.loc[titanic['Sex']=='female', 'Fare']
spst.ttest_ind(male, female)
# Ttest_indResult(statistic=-5.529140269385719, pvalue=4.2308678700429995e-08)T통계량도 -5로 많이 크고, p-value도 0에 가깝기 때문에 거의 확실히 성별에 따른 운임의 차이가 존재한다고 분석할 수 있다.
이번에는 범주값이 3개 이상인 경우를 살펴보자.
범주값이 3개 이상일 때는 t-test가 아니라 분산분석을 수행해준다.
분산분석은 ANalysis Of VAriance를 줄여서 ANOVA 라고도 부르며
전체 평균을 기준으로 전체 평균 대비 각각의 평균을 통해 여러 집단 간의 차이를 비교할 수 있다.
분산분석에서는 F통계량 값을 구해주는데 F통계량 값을 구하는 식은 다음과 같다.
𝐹 통계량 = (집단 간 분산)/(집단 내 분산) = (전체 평균 − 각 집단 평균)/(각 집단의 평균 − 개별 값)
집단 간 분산이 크고, 집단 내 분산이 작을수록 F통계량 값은 커진다.
이 때 F통계량의 값이 대략 2~3 이상이면 차이가 있다고 판단한다.
이번에는 타이타닉 데이터의 객실 등급(Pclass)에 따른 나이(Age)를 분석해보았다.
Pclass의 범주값은 1, 2, 3으로 3개이기 때문에 anova를 사용한다.
먼저 평균 비교를 위해 시각화를 해주었다.
# Pclass(3 범주) --> Age
sns.barplot(x="Pclass", y="Age", data=titanic)
plt.grid()
plt.show()
객실 등급 별 나이의 평균도 차이가 꽤 나고 신뢰구간도 겹치지 않는 것을 볼 수 있다.
이번에는 분산분석(anova) 방법으로 수치화를 해주었다.
분산분석은 spst.f_oneway( A, B, C )를 통해 수행해준다.
Pclass 별 나이를 따로 저장해준 뒤 F통계량을 구해준다.
P_1 = temp.loc[temp.Pclass == 1, 'Age']
P_2 = temp.loc[temp.Pclass == 2, 'Age']
P_3 = temp.loc[temp.Pclass == 3, 'Age']
spst.f_oneway(P_1, P_2, P_3)
# F_onewayResult(statistic=57.443484340676214, pvalue=7.487984171959904e-24)결과로 F통계량 값과 p-value를 리턴해준다.
결과를 분석해보면 F통계량이 57 정도로 매우 크고, p-value 값도 0에 가깝기 때문에 Pclass에 따른 Age는 차이가 있다고 분석할 수 있다.
분산분석 시 주의해야 할 점이 있는데,
분산분석은 전체 평균대비 각 그룹간 차이가 있는지만 알려주기 때문에 어느 그룹 간에 차이가 있는지 까지는 알 수 없다. 그래서 보통 사후분석도 진행해준다고 한다.
[ 이변량 분석 - 범주형 -> 범주형의 시각화 & 수치화 ]
범주형 -> 범주형의 관계를 분석할 때에는
- 시각화 : 100% Stacked Bar chart, 모자익 플롯 (Mosaic plot)
- 수치화 : x^2(카이제곱) 검정
을 시각화와 수치화 도구로 사용한다.
범주 vs 범주 를 비교하고 분석하기 위해서는 먼저 교차표를 만들어야 한다.
교차표는 판다스의 pd.crosstab( 행, 열 ) 문법을 사용해서 만들어 줄 수 있다.
# 두 범주별 빈도수를 교차표로 만들기
pd.crosstab(titanic['Survived'], titanic['Sex'])
# Sex female male
# Survived
# 0 81 468
# 1 233 109
pd.crosstab()에 normalize 옵션을 사용해주면 각 기준별로 0~1의 비율로 변환이 가능하다.
- columns : 열 기준 100%
- index : 행 기준 100%
- all : 전체 기준 100%
# columns : 한 칼럼의 비율의 합계가 1
pd.crosstab(titanic['Survived'], titanic['Embarked'], normalize = 'columns')
# Embarked C Q S
# Survived
# 0 0.446429 0.61039 0.660991
# 1 0.553571 0.38961 0.339009
# index : 한 행의 비율의 합계가 1
pd.crosstab(titanic['Survived'], titanic['Embarked'], normalize = 'index')
# Embarked C Q S
# Survived
# 0 0.136612 0.085610 0.777778
# 1 0.271930 0.087719 0.640351
# all : 전체의 비율의 합계가 1
pd.crosstab(titanic['Survived'], titanic['Embarked'], normalize = 'all')
# Embarked C Q S
# Survived
# 0 0.084175 0.05275 0.479237
# 1 0.104377 0.03367 0.245791
범주 -> 범주의 시각화를 할 때에는 100% Stacked Bar chart와 Mosaic plot을 사용한다.
먼저 100% Stacked Bar chart는 말 그대로 Stack의 구조로 쌓인 형태로 bar chart로 비율을 확인할 수 있는 도구이다.
먼저 교차표를 만들어주어야 하고 pd.crosstab(feature, target, normalize = 'index')
.plot.bar(stacked=True) 를 사용해준다.
다음의 순서대로 코드를 작성해주면 된다.
temp = pd.crosstab(titanic['Pclass'], titanic['Survived'], normalize = 'index')
print(temp)
temp.plot.bar(stacked=True)
plt.axhline(1-titanic['Survived'].mean(), color = 'r') # (1-생존여부의 평균) : 전체평균
plt.show()
참고로 비율만 비교해주는 것이기 때문에 양에 대한 비교는 할 수 없다.
범주 -> 범주의 또다른 시각화 도구로 Mosaic plot이 있다.
mosaic plot은 범주별 양과 비율을 그래프로 나타내 주기 때문에 100% Stacked bar 보다 전체 기준에서의 양과 비율을 직관적으로 가늠할 수 있다.
mosaic(dataframe, [ feature, target]) 을 사용해서 모자익 플롯을 그릴 수 있다.
# Pclass별 생존여부를 mosaic plot으로 그리기
mosaic(titanic, [ 'Pclass','Survived'])
plt.axhline(1- titanic['Survived'].mean(), color = 'r')
plt.show()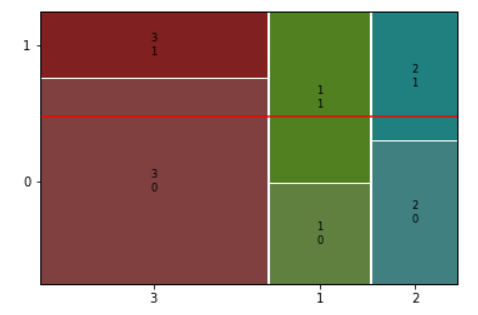
- X축 길이는 각 객실등급별 승객비율을 나타낸다.
- 그 중 3등급 객실에 대해서 보면, y축의 길이는, 3등급 객실 승객 중에서 사망, 생존 비율을 의미한다.
이렇게 얻어낸 결과에서 전체평균을 기준으로 범주별 비율의 차이가 큰지를 확인해서 범주->범주의 관계를 분석해 볼 수 있다.
만약 귀무가설이 참(범주->범주가 서로 관련이 없다.)일 경우에는 다음과 같이 전체평균을 기준으로 범주 별 비율의 차이가 없는 그림이 나올 것이다.
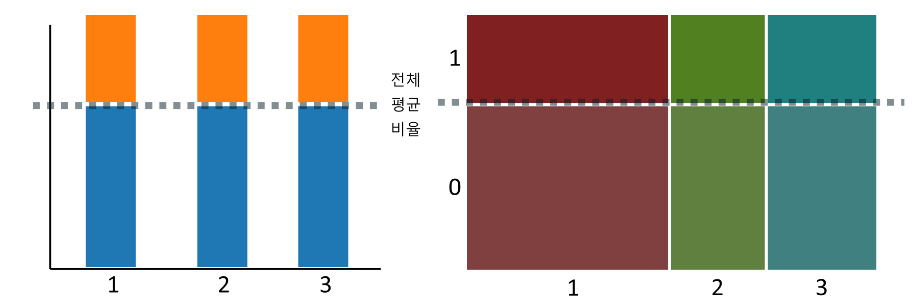
범주->범주의 수치화 분석 도구로는 카이제곱 검정을 사용한다.
카이제곱 검정은 범주형 변수들 사이에 어떤 관계가 있는지, 수치화 하는 방법으로
공식은 다음과 같다.

- (x 변수의 자유도) × (y 변수의 자유도)
- 예 : Pclass --> Survived
- Pclass : 범주가 3개, Survived : 2개
- (3-1) * (2-1) = 2
- 그러므로, 2의 2 ~ 3배인 4 ~ 6 보다 카이제곱 통계량이 크면, 차이가 있다고 볼수 있음.
타이타닉 데이터에서 객식등급과 생존여부 간의 카이 제곱 검정을 수행해 보았다.
먼저 교차표를 만들어서 집계를 해 주어야 하는데, normalize 옵션은 사용하지 않는다.
pd.crosstab(titanic['Survived'], titanic['Pclass'])
# Pclass 1 2 3
# Survived
# 0 80 97 372
# 1 136 87 119카이제곱 검정은 spst.chi2_contingency( table ) 로 수행할 수 있으며 결과로 카이제곱통계량, p-value, 자유도, 기대빈도를 리턴한다.
# 먼저 집계
table = pd.crosstab(titanic['Survived'], titanic['Pclass'])
print('교차표\n', table)
print('-' * 100)
# 카이제곱검정
result = spst.chi2_contingency(table)
print('카이제곱통계량 :', result[0])
print('p-value :', result[1])
print('자유도 :', result[2])
print('기대빈도 :\n',result[3])
결과를 분석해보면 카이제곱 통계량이 102 정도로 자유도 2의 3배인 6보다 훨씬 큰 값을 가지고 있고, p-value 또한 0에 가까운 값이기 때문에 객실등급별 생존여부는 관련이 많이 있다고 분석해 볼 수 있다.
[ 이변량 분석 - 숫자형 -> 범주형의 시각화 & 수치화 ]
숫자형 -> 범주형의 관계를 분석할 때에는
- 시각화 : 그룹별 히스토그램(histogram), 그룹별 밀도함수그래프(kde plot)
- 수치화 : (로지스틱 회귀)
을 시각화와 수치화 도구로 사용한다.
숫자형 -> 범주형의 관계를 분석할 때에는 시각화 도구로 다음의 두 가지 방법이 사용 가능하다.
- 히스토그램을 범주별로 겹쳐 그린 후 비교
- 밀도함수 그래프(KDE plot)를 범주별로 겹쳐 그린 후 비교
히스토그램은 숫자형 데이터의 단변량 분석 시 사용했던 seaborn 라이브러리의 sns.hisplot()에서 hue로 범주 별 옵션을 지정해주면 된다.
# 나이에 따른 생존여부를 히스토그램으로 겹쳐 보기
sns.histplot(x='Age', data = titanic, hue = 'Survived')
plt.show()
밀도함수 그래프는 sns.kdeplot()으로 그릴 수 있는데 옵션을 통해 여러 방식으로 그려볼 수가 있다.
- kdeplot( , hue = 'Survived')
- 생존여부의 비율이 유지된 채로 그려짐
- 두 그래프의 아래 면적의 총 합이 1
- kdeplot( , hue = 'Survived', common_norm = False)
- 생존여부 각각 아래 면적의 합이 1인 그래프
- kdeplot( , hue = 'Survived', multiple = 'fill')
- 나이에 따라 생존여부 비율을 비교해볼 수 있음. (양의 비교가 아닌 비율!)
- 두 그래프의 아래 면적 총 합이 1이 되도록 그리기
# 두 그래프의 아래 면적 총 합이 1
sns.kdeplot(x='Age', data = titanic, hue ='Survived')
plt.show()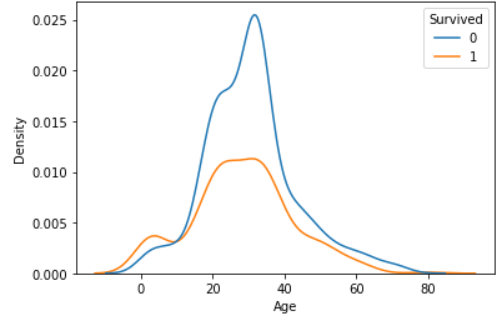
- 두 밀도함수 그래프의 아래 면적이 각각 1이 되도록 그리기 ( common_norm = False )
# 두 그래프의 아래 면적이 각각 1
sns.kdeplot(x='Age', data = titanic, hue ='Survived', common_norm = False)
plt.show()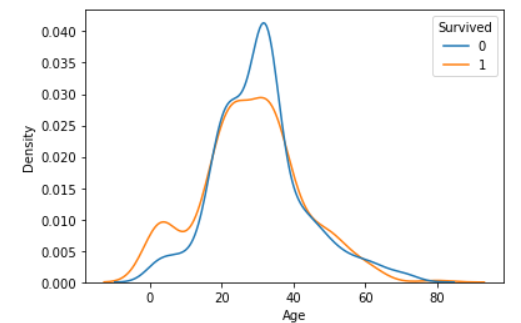
- 두 밀도함수 그래프의 비율로 비교 ( multiple = 'fill' )
# 비율로 비교
sns.kdeplot(x='Age', data = titanic, hue ='Survived'
, multiple = 'fill')
plt.axhline(titanic['Survived'].mean(), color = 'r')
plt.show()
- 히스토그램으로도 비율 비교가 가능하다.
sns.histplot(x='Age', data = titanic, bins = 16
, hue ='Survived', multiple = 'fill')
plt.axhline(titanic['Survived'].mean(), color = 'r')
plt.show()
시각화를 통해 숫자->범주의 관계를 파악할 때에는 범주별로 나눈 두 그래프를 겹쳐 그렸을 때 서로 일치할수록 차이가 없는 것이 된다.
숫자형 -> 범주형의 경우에는 로지스틱 회귀 모델로부터 p-value를 구한다.
- 귀무가설 : 해당 변수의 회귀계수가 0이다. (범주형 Y와 관련이 없다.)
- 대립가설 : 해당 변수의 회귀계수가 0이 아니다. (관련이 있다.)
로지스틱 검정을 수행하기 위해서는 y가 0,1로 되어 있어야 한다!!
import statsmodels.api as sm
model = sm.Logit(titanic['Survived'], titanic['Age'])
result = model.fit()
print(result.pvalues)
# Optimization terminated successfully.
# Current function value: 0.661967
# Iterations 4
# Age 3.932980e-13
# dtype: float64Age의 옆에 나온 숫자가 p-value이다.
이렇게 지난 시간에 이어서
- 숫자형 --> 숫자형
- 범주형 --> 숫자형
- 범주형 --> 범주형
- 숫자형 --> 범주형
4가지 경우의 가설검증을 수행해주는 시각화, 수치화 도구들을 사용해보았다.
최종적으로 다시 한 번 각각의 도구들을 정리한 표를 보면서 정리해보자
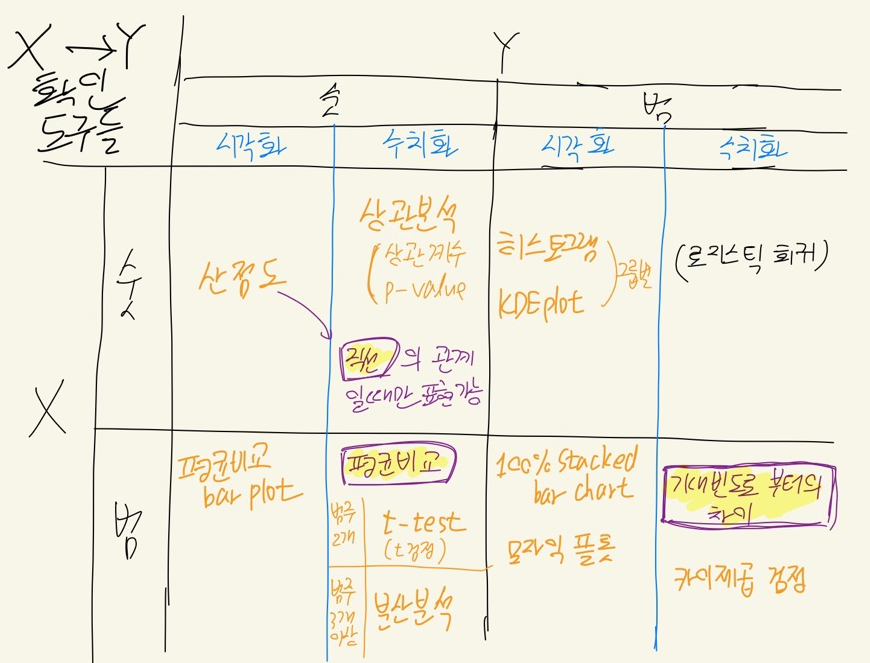
각각의 사용법을 벌써부터 다 외우는 것은 어려울 것이다. 코드를 외우지는 않더라도 각각의 경우에 따라 어떤 시각화, 수치화 도구가 필요한지를 파악하고 코드는 그 이후에 찾아보도록 하자.
현재 분석하고자 하는 변수들이 숫자형인지 범주형인지를 확인해보고, 변수들의 개별 분석을 수행한 뒤 내가 세운 가설을 검증하기 위해 위에서 정리한 도구들을 찾아서 사용하는 능력을 기르는 것이 중요하다.
우리가 가설검증에 사용되는 도구들을 활용해서 얻은 결과를 무조건적으로 믿고 정답을 맞추는 것이 중요한 것이 아니다. 모든 도구는 완벽하지 않기 때문에 우리가 세운 가설을 검증하기 위한 참고자료로 사용하는 것이지 맹목적으로 도구의 결과만을 보고 강한 관계인지 아닌지를 결정지을 필요가 없다. 우리는 이 과정에서 비즈니스를 더 잘 파악하기 위해 데이터를 이해하고 있는 것이다.
추가로 아래는 추가로 다변량 분석의 각 경우 별로 시각화를 했을 경우
귀무가설이 참일 때 어떤 그림인지를 정리해보았다.

'KT AIVLE School' 카테고리의 다른 글
| (5주차 - 22.08.22) 머신러닝1 - 선형회귀,회귀모델평가 (0) | 2022.08.22 |
|---|---|
| (4주차 - 22.08.16~22.08.19) 미니프로젝트1 (0) | 2022.08.22 |
| (3주차 - 22.08.11) 데이터 분석 및 의미 찾기 2 - Seaborn,이변량분석1 (0) | 2022.08.12 |
| (3주차 - 22.08.10) 데이터 분석 및 의미 찾기 1 (0) | 2022.08.10 |
| (3주차 - 22.08.09) 데이터 처리2 (0) | 2022.08.09 |
