[ 오늘 배운 내용 ]
1. 일반화 성능
- 성능 향상을 위한 노력
a. 성능의 평균으로 계산 : 무작위 샘플링, K-Fold Cross Validation (계획적 방식)
b. 데이터 늘리기 (variance, bias 감소) : Learning Curves, Elbow Method
c. 튜닝하기 (bias 감소, 과적합 피하기)
2. 모델 복잡도와 과적합
- Underfitting(과소적합), Overfitting(과대적합)
- 단순한 모델, 복잡한 모델
- 적절한 모델 찾기 : 모델의 복잡도
3. 앙상블 (Ensemble)
- Bagging (Bootstrap + Aggregating)
- Random Forest : Row random, Feature random
- Boosting
- Gradient Boost - XGBoost
1. 일반화 성능
모든 데이터셋은 모집단의 부분집합이라고 보면 된다.
모델링의 목표는 부분집합을 학습해서 모집단을 적절히 예측하는 것(적절한 성능을 얻는 것)이다.
모델의 성능을 향상시키기 위한 노력들은 크게 봤을 때 다음의 3가지가 있다.
- 성능의 평균으로 계산 : 무작위 샘플링, K-Fold Cross Validation (계획적 방식)
- 데이터 늘리기 (variance, bias 감소) : Learning Curves, Elbow Method
- 성능 튜닝하기 (bias 감소, 과적합 피하기) : 그리드서치, 랜덤서치를 활용한 하이퍼파라미터 튜닝
[ 1. 성능의 평균으로 계산 ]
같은 모델을 하이퍼파라미터도 수정하지 않고 데이터만 바꿔서 학습시켜도 성능이 다르게 나온다. 예를 들어 어떤 모델을 한 데이터셋에 대해 학습시켰을 때 좋지 않은 성능이 나왔는데, 같은 모델을 다른 데이터셋에 다시 학습시켜봤을 때는 갑자기 좋은 성능이 나올 수도 있다.
이렇게 데이터에 따라서 들쑥날쑥한 성능이 나오는 Variance(편차)를 줄이기 위해 한 모델을 여러번 샘플링한 데이터에 대해 테스트 해보고 각 테스트 마다의 성능의 평균으로 계산을 해줄 수 있다. (특정 알고리즘, 특정 하이퍼파라미터값 등의 조건을 고정시킨 채로)
성능의 평균을 계산하기 위해 데이터를 여러번 샘플링하는 방법은 두가지가 있다.
- 방법1 : 무작위 샘플링
- 방법2 : 계획적 샘플링 (K-Fold Cross Validation)
무작위 샘플링 방법은 무작위로 train, validation 데이터를 뽑아서 여러번 모델링을 반복 실행한 뒤 각각의 성능의 평균으로 계산해주는 방법이다.
그냥 특정 모델을 특정 데이터셋에 대해서 같은 코드로 여러번 실행해보는데, 매 시도마다 train, val 데이터를 새로 split 해준다. 그리고 그 결과의 성능들의 평균과 표준편차를 내준 뒤 분포를 확인해보면 정규분포의 모양을 갖는데 코드로 한번 확인해보자.
아래 코드에서는 의사결정트리 모델을 특정 데이터셋에 대해 스플릿+실행의 과정을 100번 반복했을 때의 각각의 성능을 result 리스트에 담아준다.
# 100번 반복 실행
result = []
for i in range(100):
x_train, x_val, y_train, y_val = train_test_split(x, y, test_size=.2)
model = DecisionTreeClassifier(max_depth = 3)
model.fit(x_train, y_train)
pred = model.predict(x_val)
result.append(accuracy_score(y_val, pred))
평균과 표준편자를 확인해보고, 결과를 시각화해보니 정규분포의 모양을 갖는 것을 볼 수 있다.
print('mean:', np.mean(result), ', std:', np.std(result))
sns.kdeplot(result)
plt.axvline(np.mean(result), color = 'r')
plt.grid()
plt.show()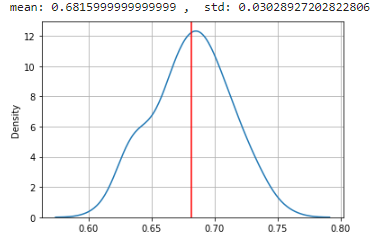
따라서 한번만 모델링 해본 결과의 성능으로 이야기하는 것이 아니라, 여러번 수행해본 뒤의 평균으로 성능을 판단해주어야 한다.
하지만 이보다는 주로 2번째 방법인 계획적 샘플링을 많이 사용하기 때문에 무작위 샘플링은 이정도만 확인해보고 아래의 내용에 초점을 맞춰보자.
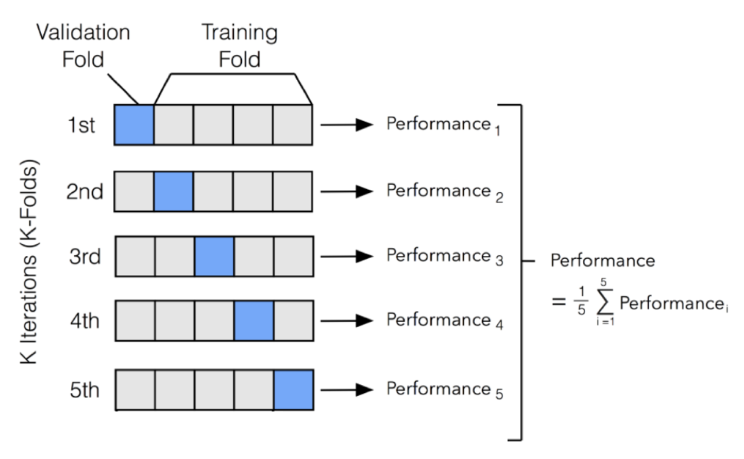
계획적으로 데이터를 샘플링 하는 방법인 K-Fold Cross Validation 기법을 일반적으로 데이터 샘플링 시에 많이 사용한다.
k-fold cross validation에서는 모든 데이터가 한번씩은 validation 용으로 사용되도록 데이터를 k등분해서 k번 수행하고, 이 각각의 수행들의 평균 성능으로 평가를 수행한다.
아래 그림과 같이 데이터를 k등분 해준 뒤 각 등분된 데이터를 한번씩 validation으로, 나머지를 train 데이터로 사용해보면서 모델링한 각각의 모델의 성능의 평균을 구해주는 것이다.
따라서 k-fold 교차검증 시에는 모든 데이터가 한번씩은 validation 데이터로 들어가서 사용이 된다는 장점이 있다.
[ k-fold cross validation 실습 코드 ]
- cross_val_score() 함수 로딩
# 필요한 패키지, 함수 로딩
from sklearn.model_selection import cross_val_score
- 모델링 및 cross validation (교차 검증)
# 모델 선언
model = DecisionTreeClassifier(max_depth = 3)
# train + validation set을 이용하여 학습, 예측, 평가를 한번에. (여기서는 .fit 이 아님!)
dt_result = cross_val_score(model, x, y, cv=10)
print(dt_result)
print(dt_result.mean(), dt_result.std())
# [0.66 0.73 0.64 0.68 0.66 0.72 0.63 0.69 0.61 0.73]
# 0.675 0.040311288741492736사용하려는 모델을 선언해준 뒤 .fit()이 아니라 cross_val_score()를 사용한다. 여기서 교차검증으로 데이터를 train, validation으로 나눠주기 때문에 train용으로 나눈 데이터가 아니라 x,y를 그대로 넣어준다.
cv=10으로 지정해준 값은 k-fold cross validation의 k값을 의미한다. (k값은 보통 5~10 사이에서 많이 사용된다.)
cross_val_score 함수는 k만큼 샘플링해서 모델을 테스트한 성능을 리스트로 반환해주고, 이 결과의 평균을 통해 개별 모델의 평균 성능을 확인해볼 수 있다.
[ 2. 데이터 늘리기 ]
일반적으로 training set의 크기가 커지면, 즉 데이터가 많아지면 모델 성능이 향상된다.
데이터의 양을 늘리면 다음의 두가지 효과를 동시에 얻을 수 있다.
- Variance(편차) 감소 : 오락가락하지 않는 성능을 얻게 된다.
- Bias(오차) 감소 : accuracy가 좋아진다.
데이터의 양에 따른 성능의 경향을 볼 수 있는 그래프가 Learning Curves 이다.
sklearn.model_selection의 learning_curve() 함수를 사용하여 러닝커브를 확인해볼 수 있다.
# learning_curve() 함수 불러오기
from sklearn.model_selection import learning_curve
model = DecisionTreeClassifier(max_depth = 3) # 모델선언
x.shape[0] # 4000건의 train set
# 4000
# 러닝커브
tr_size, tr_scores, val_scores = learning_curve(model, x, y
, train_sizes = range(5, 3200, 10) # 데이터를 어떻게 늘려갈지 설정
, cv = 5)
[ learning_curve() 함수 Input ]
- 모델, x, y
- train_sizes = 순차적으로 늘려가며 학습시킬 데이터 양의 리스트
- cv = cross validation 설정
[ learning_curve() 함수 Output]
- tr_size : Input에서 지정한 값리스트(train_sizes)
- tr_scores : 학습용 데이터에서의 성능
- val_scores : validation 성능
val_scores로 validation 성능을 확인해보면 위에서 cv=5로 지정해줬기 때문에 각 데이터 양 별로 5-fold cross validation을 수행한 5개씩의 결과를 확인할 수 있다.
val_scores[:5]
# array([[0.5125 , 0.47625, 0.495 , 0.48625, 0.51 ],
# [0.6 , 0.4975 , 0.4975 , 0.45875, 0.485 ],
# [0.5325 , 0.52375, 0.56 , 0.5675 , 0.5625 ],
# [0.505 , 0.5525 , 0.56 , 0.55875, 0.57625],
# [0.50375, 0.54 , 0.55625, 0.58875, 0.5825 ]])
각 데이터 양 별 교차검증한 결과를 평균으로 저장하고 이를 시각화해서 확인해보았다.
# 각 데이터 양 별 cv한 결과를 평균으로 집계
val_scores_mean = val_scores.mean(axis = 1)
# 시각화
plt.figure(figsize = (10,6))
plt.plot(tr_size, val_scores_mean)
plt.ylabel('val_accuracy')
plt.xlabel('train_size')
plt.grid()
plt.show()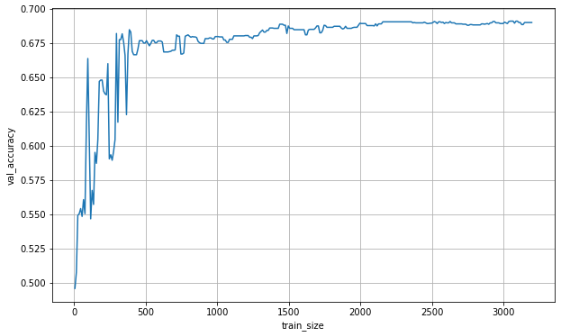
- 데이터 양이 많아질수록 Bias(오차)는 감소하면서 accuracy 성능이 좋아지는 것을 볼 수 있다.
- 하지만 성능이 개선되다가 어느 지점부터는 성능 개선 효과가 급격히 줄어들게 된다.
- 뒤로 갈수록 점점 성능 개선 정도에는 차이가 없지만 데이터가 많은 만큼 모델링 속도는 더 늦어지게 될 것이다.
위의 분석 내용으로 미루어 보니 데이터가 많다고 해서 무조건 좋다고 보기는 힘들다.
따라서 데이터는 적당히 많이야 하고 이 적당히 많은 데이터의 기준은 Learning Curve 그래프에서 Elbow Method라는 기법을 참고해서 정해볼 수 있다.
Elbow Method는 팔꿈치 지점 근방을 적절한 값으로 보는 기법으로 적절한 지점을 찾기 위한 간편한 추론 방법이다.
따라서 팔꿈치 기법에 기반하여 위의 러닝커브 그래프를 분석해보면 500, 1500 등의 지점이 적절한 데이터의 양이라고 생각해볼 수 있다. 하지만 사실 1500개 정도의 데이터도 계산이 금방 되기 때문에 더 많은 값을 고려해봐도 문제는 없다.
추가로 val_scores의 각 데이터 양 별 교차검증한 결과의 표준편차를 구해서 Variance의 변화도 시각화하여 확인해보았다.
# 데이터 양 별 cv한 결과의 표준편차
val_scores_std = val_scores.std(axis = 1)
# 시각화
plt.figure(figsize = (10,6))
plt.plot(tr_size, val_scores_std)
plt.ylabel('Variance(val_accuracy)')
plt.xlabel('train_size')
plt.grid()
plt.show()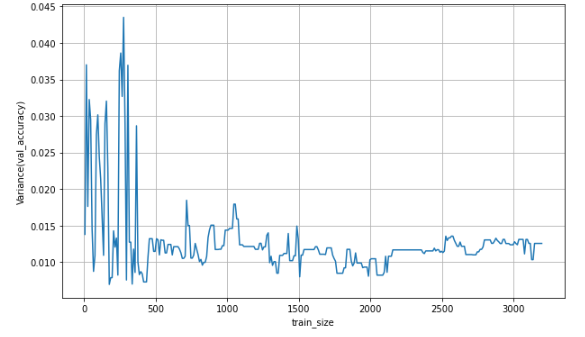
데이터가 많아질수록 성능의 변동(편차)가 작아지는 것을 확인해볼 수 있다.
2. 모델 복잡도와 과적합
- Overfitting(과대적합) : 모델링을 수행할 때 train set에 모델을 과하게 맞추어서 새 데이터에 대해서 성능이 떨어지는 경우
- Underfitting(과소적합) : 모델의 학습이 너무 안 된 경우
모델을 train set에 너무 맞춰도 좋지 않고, 너무 맞추지 않아도 좋지 않다. 따라서 우리는 그 사이 가장 적절한 모델을 찾아내야 한다.
[ 모델의 복잡도 ]
: train set의 패턴이 반영된 정도
- 모델의 복잡도 높음(복잡한 모델) --> 오버피팅
- 모델의 복잡도 낮음(단순한 모델) --> 언더피팅
단순한 모델
- 대충, 적당히 학습한 모델
- 가장 단순한 모델 : y의 평균으로 예측하는 평균 모델
복잡한 모델
- 학습 데이터를 하나하나 모두 반영한 모델
- 가장 복잡한 모델 : train set의 모든 패턴이 반영된 모델
우리는 적절한 복잡도의 모델을 찾기 위해 모델의 복잡도를 적절하게 조절해야 한다.
(모델의 복잡도 : 학습용 데이터의 패턴을 반영하는 정도)
==> 알고리즘 마다 이 복잡도를 조절할 수 있는 방법이 있는데, 주로 하이퍼파라미터 튜닝을 통해 해결이 가능하다.
[ 선형모델의 복잡도 ]
Training set에 있는 속성(변수)를 많이 사용할수록 Training set에 대한 모델 정확도가 향상될 가능성이 높다. (복잡도가 높아진다.)
[ 트리모델의 복잡도 ]
- 나무 크기가 클 수록 복잡하다.
- max_depth(트리의 최대 깊이) : 값이 클수록 복잡
- min_samples_leaf(리프노드 당 최소 데이터 건수) : 값이 작을수록 복잡
[ SVM의 복잡도 ]
- Cost(오차를 줄이기 위한 비용) : 값이 클수록 복잡
- gamma : 값이 클수록 복잡
모델의 적절한 복잡도를 찾기 위해서 적합도 그래프(Fitting Graph)를 그려보자
의사결정트리모델을 max_depth값을 1부터 20까지 실행해보며 각각의 모델들에 대해 train데이터와 validation 데이터에 대한 정분류율(accuracy)을 구해서 리스트로 저장하고 확인해보았다.
result_train = [] # train set을 가지고 예측한 결과
result_val = [] # val set을 가지고 예측한 결과
depth = list(range(1,21))
for d in depth :
model = DecisionTreeClassifier(max_depth = d)
model.fit(x_train, y_train)
pred_tr, pred_val = model.predict(x_train), model.predict(x_val)
result_train.append(accuracy_score(y_train, pred_tr))
result_val.append(accuracy_score(y_val, pred_val))
pd.DataFrame({'max_depth': list(range(1,21)),'train_acc':result_train, 'val_acc':result_val})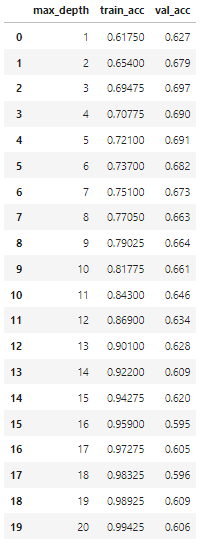
의사결정트리는 나무의 크기가 클 수록 복잡한 모델이기 때문에 크기를 결정하는 max_depth가 커질수록 train set에 대한 정분류율은 높아지고, validation set에 대한 정분류율은 높아지다가 다시 낮아지는 것을 볼 수 있다.
이를 시각화해보면
plt.figure(figsize = (12,8))
plt.plot(depth, result_train, label = 'train_acc', marker = 'o')
plt.plot(depth, result_val, label = 'val_acc', marker = 'o')
plt.xlabel('Complexity')
plt.ylabel('Accuracy')
plt.legend()
plt.grid()
plt.show()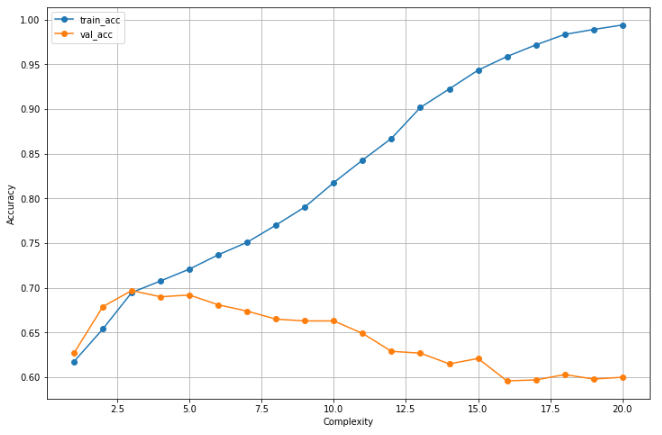
위와 같은 적합도 그래프를 볼 수 있다.
train set에 대한 정확도는 계속 높아지는 반면 validation set에 대한 정확도가 낮아지기 시작하면 오버피팅(과적합)이 되고 있다고 생각할 수 있다.
따라서 우리는 과적합 지점을 찾아야 하는데 다음의 3가지를 고려해서 찾아준다.
- train과 validation의 성능이 급격히 벌어지는 지점
- validation 성능의 고점
- 가능한 한 단순한 모델
1번과 3번은 사실 주관적인 요소기 때문에 1과 3을 기반으로 해서 2번 validation 성능이 가장 좋게 나오는 지점 주변을 적정 지점으로 사용하는 것이 좋다.
[ 오버피팅(과적합)을 피해야 하는 이유 ]
모델이 복잡해지면 가짜 패턴(연관성)까지 학습하게 된다. 가짜 패턴은 학습 데이터에만 존재하는 특이한 성질로 모집단 전체의 특성이 아니기 때문에 학습 데이터 이외의 데이터셋에서는 모델의 성능이 떨어지게 만든다.
우리가 모델링을 하는 목적은 학습용 데이터에 있는 패턴으로 그 외의 데이터(모집단 전체)를 예측하는 것이다.
따라서 학습한 패턴은 학습용 데이터를 잘 설명하는 동시에 새로운 데이터도 잘 예측할 수 있어야 한다.
이를 위해 우리는 적절한 복잡도로 적절한 예측력을 갖는 (validation 입장에서 최고의 성능을 낼 수 있는) 모델을 만들어내야 한다.
3. 앙상블 (Ensemble)
앙상블 기법은 여러 모델을 가지고 종합적으로 성능을 판단하는 기법이다.
[ 앙상블의 종류 ]
- Bagging
- Boosting
- Stacking
[ Bagging (Bootstrap + Aggregating) ]
Bagging 기법은 Bootstrap와 Aggregating이 합쳐진 말로,
Bagging에서는 데이터를 무작위로 뽑고, 뽑은 데이터는 다시 데이터셋에 돌려놓는 복원추출을 여러번 수행하는 Bootstrap sampling(부트스트랩 샘플링)을 수행하고, 각각의 Bootstrap sample에 대해서 모델링한 예측 결과를 집계하여 평균을 내준다.(Aggregating)
[ Random Forest (랜덤 포레스트) ]
랜덤 포레스트는 배깅의 한 종류로 트리 모델을 기반으로 하는 알고리즘이다.
지정한 수만큼의 의사결정트리 모델을 실행한 뒤, 각 모델의 예측값의 평균으로 최종 예측을 수행한다.
랜덤 포레스트 사용 시, 행과 변수에 무작위성이 부여되어서 조금씩은 다른 트리들이 생성되기 때문에 집단지성을 활용하게 되어 신뢰 가능한 결과를 얻을 수 있다.
랜덤 포레스트에서 데이터를 랜덤하게 샘플링 하는 방법은 두가지가 있다.
- Row에 대한 랜덤 : 랜덤하게 각 데이터를 샘플링
- Feature에 대한 랜덤 : 각 트리에서 가지를 split할 때, 기준이 되는 feature를 랜덤하게 선정
참고로 split의 기준이 될 feature들을 데이터셋의 feature수와 동일하게 설정하면 만들어진 여러 모델들이 모두 비슷하기 때문에 큰 의미가 없을 수 있다.
Feature를 무작위로 지정한 n개 만큼 뽑게 되면 트리가 split을 할 때 다음의 과정을 거친다.
- 무작위로 뽑힌 n개의 feature들에 대해
- 불순도로부터 정보전달량(부모불순도 - 자식불순도)을 계산한다.
- 가장 정보전달량이 큰 feature를 선정하여 split
랜덤포레스트 모델은 sklearn.ensemble의 RandomForestClassifier() 를 사용해서 선언한다.
from sklearn.ensemble import RandomForestClassifier
- 모델 선언, 학습, 예측, 평가
model = RandomForestClassifier(n_estimators = 5, max_depth = 3) # 모델(트리)의 개수 5개
model.fit(x_train, y_train)
pred = model.predict(x_val)
print(classification_report(y_val, pred))
# precision recall f1-score support
#
# 0 0.67 0.71 0.69 769
# 1 0.68 0.63 0.65 731
#
# accuracy 0.67 1500
# macro avg 0.67 0.67 0.67 1500
# weighted avg 0.67 0.67 0.67 1500n_estimators : 모델(트리)의 개수 설정
위의 코드에서는 5개의 의사결정트리 모델을 만들었다. .estimators_를 사용해서 각 트리를 확인해볼 수도 있다.
# 5개의 decision tree 모델 (인덱스 지정해주면 원하는 모델 갖고올 수 있음)
model.estimators_
# [DecisionTreeClassifier(max_depth=3, max_features='auto',
# random_state=1844359340),
# DecisionTreeClassifier(max_depth=3, max_features='auto', random_state=608549849),
# DecisionTreeClassifier(max_depth=3, max_features='auto',
# random_state=1431771941),
# DecisionTreeClassifier(max_depth=3, max_features='auto', random_state=433859175),
# DecisionTreeClassifier(max_depth=3, max_features='auto',
# random_state=1334892434)]
변수 중요도도 각 모델들의 중요도를 평균내서 확인이 가능하다. ( .feature_importances_ )
# 변수 중요도
print(x_train.columns)
print(model.feature_importances_) # 각 모델들의 중요도를 평균내서 구해줌
# Index(['COLLEGE', 'INCOME', 'OVERAGE', 'LEFTOVER', 'HOUSE', 'HANDSET_PRICE',
# 'OVER_15MINS_CALLS_PER_MONTH', 'AVERAGE_CALL_DURATION',
# 'REPORTED_SATISFACTION_sat', 'REPORTED_SATISFACTION_unsat',
# 'REPORTED_SATISFACTION_very_sat', 'REPORTED_SATISFACTION_very_unsat',
# 'REPORTED_USAGE_LEVEL_high', 'REPORTED_USAGE_LEVEL_little',
# 'REPORTED_USAGE_LEVEL_very_high', 'REPORTED_USAGE_LEVEL_very_little',
# 'CONSIDERING_CHANGE_OF_PLAN_considering',
# 'CONSIDERING_CHANGE_OF_PLAN_never_thought',
# 'CONSIDERING_CHANGE_OF_PLAN_no', 'CONSIDERING_CHANGE_OF_PLAN_perhaps'],
# dtype='object')
# [0.00000000e+00 6.38051016e-02 6.85345704e-02 0.00000000e+00
# 4.39165256e-01 6.06199715e-02 2.42904087e-01 1.09817035e-01
# 0.00000000e+00 1.90101777e-03 3.93927458e-03 0.00000000e+00
# 5.32281391e-03 0.00000000e+00 0.00000000e+00 1.07413067e-03
# 1.62679731e-03 0.00000000e+00 1.24226535e-03 4.76789376e-05]
랜덤 포레스트 모델의 성능을 결정하는 하이퍼파라미터는 트리의 수를 지정하는 n_estimator와, split 대상이 되는 feature의 개수인 max_features가 있다.
다른 모델처럼 랜덤 포레스트에서도 그리드서치나 랜덤서치 등의 방법으로 적절한 트리의 개수를 찾아내는 것이 중요하다.
랜덤포레스트는 트리가 많아진다고 해서 모델이 복잡해지지 않는다.
평균을 사용하기 때문에 이상치들은 대세에 묻혀서 전체 관점에 영향을 줄 수 없게 되기 때문에 트리가 적당히 많아지면 오히려 과적합을 회피해준다.
그리고 주요 하이퍼파라미터들을 기본값으로 지정해도 괜찮은 성능의 모델이 만들어지기 때문에 디폴트 값으로 써도 충분하다. (n_estimators의 디폴트값은 100, max_features의 디폴트값은 전체feature의 수에 루트를 씌운 값)
성능이 좋은 알고리즘이기 때문에 현장에서도 많이 쓴다고 한다.
[ Boosting - XGBoost ]
Boosting이란 여러 트리 모델을 결합해서 오차를 줄이는 모델을 구성하는 방식이다.
모델(트리)의 개수에 따라 예측 결과가 달라진다. (성능이 달라짐)
점점 홀을 향해 가까워지도록 공을 치는 골프와 비슷하게 생각할 수 있다.
Boosting의 종류 중 하나인 XGBoost 알고리즘의 내부 작동(. fit() ) 원리는 다음과 같다.
- 예측을 수행하기 위한 트리 모델을 만들고 예측한 값과 정답과의 오차를 구한다.
- 그 다음 앞서 구한 오차를 예측하는 모델을 만들고 원래 오차와 예측한 오차와의 오차를 구한다.
- 2.의 과정을 반복하며 계속해서 오차를 줄여간다.
- 지정된 개수 만큼의 모델을 다 만들면 초기 예측값에 이후 예측한 오차값들을 더한 최종예측값을 얻어낸다.
과정을 더 간단하게 정리하면 다음과 같다.
- 복수의 트리를 순차적으로 만들어서 예측
- 오차를 줄이는 방향으로 트리(모델)를 반복 생성
- 트리들을 모두 더해서 하나의 모델로
계속해서 모델을 붙여나가는 방식이기 때문에 Adaptive Model이라고도 한다.
[ XGBoost의 주요 파라미터 ]
- learning_rate : 가중치 조정 비율 ( = 붙인 모델의 적용 비율. 딥러닝의 학습률과 비슷) 0~1사이 값
- max_depth : 트리의 최대 깊이
- n_estimators : iteration 횟수 (= 모델의 개수 = 오차를 줄이려는 시도 횟수)
max_depth 값은 커질수록 트리가 커지기 때문에 모델이 복잡해진다.
n_estimators 역시 커질수록 오차를 줄이려는 시도가 많아지는 것이기 때문에 모델이 복잡해질 수 있다.
XGB에는 자체적으로 과적합을 방지하기 위한 규제가 포함되어 있기에 크게 validation 성능이 떨어지지는 않지만 과적합의 위험이 있다는 것은 알고 있자
- XGBoost 분류 모델 : XGBClassifier()
- XGBoost 회귀 모델 : XGBRegressor()
[ XGBoost 실습 코드 ]
- XGBoost는 sklearn에서 불러오지 않는다.
from xgboost import XGBClassifier, plot_tree
- 모델 선언, 학습, 예측, 평가
# 모델 선언
model = XGBClassifier(n_estimators = 5)
# 학습
model.fit(x_train, y_train)
# 예측
pred = model.predict(x_val)
# 평가
print(classification_report(y_val, pred))
# precision recall f1-score support
#
# 0 0.72 0.66 0.69 769
# 1 0.67 0.72 0.70 731
#
# accuracy 0.69 1500
# macro avg 0.69 0.69 0.69 1500
# weighted avg 0.69 0.69 0.69 1500사용법은 다른 모델들과 똑같다.
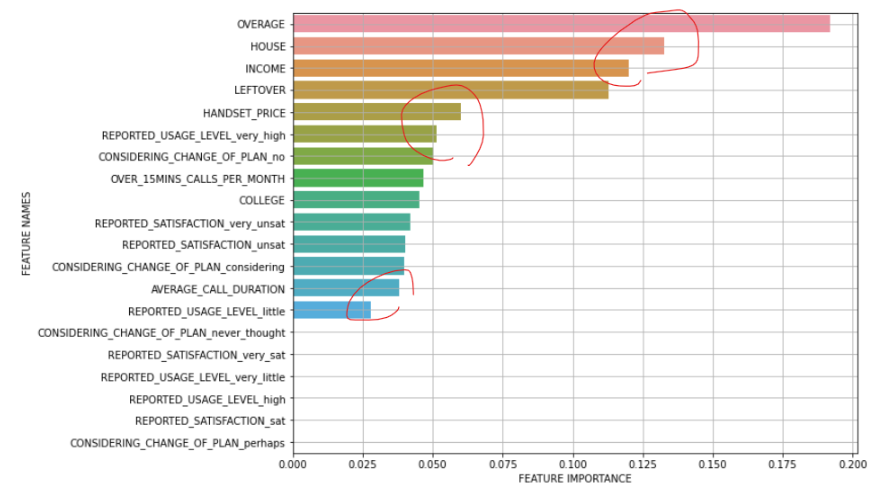
- 변수 중요도 확인 (.feature_importances_)
# 변수 중요도
print(x_train.columns)
print(model.feature_importances_)
# Index(['COLLEGE', 'INCOME', 'OVERAGE', 'LEFTOVER', 'HOUSE', 'HANDSET_PRICE',
# 'OVER_15MINS_CALLS_PER_MONTH', 'AVERAGE_CALL_DURATION',
# 'REPORTED_SATISFACTION_sat', 'REPORTED_SATISFACTION_unsat',
# 'REPORTED_SATISFACTION_very_sat', 'REPORTED_SATISFACTION_very_unsat',
# 'REPORTED_USAGE_LEVEL_high', 'REPORTED_USAGE_LEVEL_little',
# 'REPORTED_USAGE_LEVEL_very_high', 'REPORTED_USAGE_LEVEL_very_little',
# 'CONSIDERING_CHANGE_OF_PLAN_considering',
# 'CONSIDERING_CHANGE_OF_PLAN_never_thought',
# 'CONSIDERING_CHANGE_OF_PLAN_no', 'CONSIDERING_CHANGE_OF_PLAN_perhaps'],
# dtype='object')
# [0.04530415 0.12009237 0.19194081 0.11272172 0.13279922 0.06022841
# 0.04685733 0.03811195 0. 0.04008486 0. 0.04205307
# 0. 0.02807601 0.05156877 0. 0.0399426 0.
# 0.05021862 0. ]
아래 그림은 위에서 확인해본 변수 중요도를 시각화해본 것인데, 어떤 변수가 중요한지 판단할 때에도 엘보우 메서드를 활용해서 확 바뀌는 지점에서 끊어줄 수 있다.
[ Stacking ]
Stacking 은 간단하게 말하면 다른 모델로 예측한 예측값을 다시 다른 모델의 x로 집어넣어주는 기법이다.
수업시간에는 다루지 않았지만 참고자료 활용해서 공부해보자
(추가공부 카테고리에 정리함)
'KT AIVLE School' 카테고리의 다른 글
| (6주차 - 22.08.29) 머신러닝6 - 시계열 분석 (0) | 2022.08.29 |
|---|---|
| (5주차 - 22.08.26) 머신러닝5 - 비지도학습 (0) | 2022.08.26 |
| (5주차 - 22.08.24) 머신러닝3 - 결정트리,SVM,모델성능튜닝 (0) | 2022.08.25 |
| (5주차 - 22.08.23) 머신러닝2 - KNN,로지스틱회귀,분류모델평가 (0) | 2022.08.23 |
| (5주차 - 22.08.22) 머신러닝1 - 선형회귀,회귀모델평가 (0) | 2022.08.22 |
