[ 오늘 배운 내용 ]
1. 회귀, 분류 알고리즘 : KNN (K-Nearest Neighbors)
- Scaling (스케일링)
- knn의 거리 계산법
2. 분류 알고리즘 : Logistic Regression (로지스틱 회귀)
- 회귀계수 해석
3. 분류 모델의 평가 방법
- 교차표 (Confusion Matrix)
- 성능지표
- 전체 관점 : Accuracy (정분류율)
- 특정 class 관점 : Recall (재현율), Precision (정밀도), F1_Score
1. KNN (K-Nearest Neighbor)
KNN 알고리즘은 분류와 회귀 문제에서 모두 사용 가능한 알고리즘으로 거리를 계산하여 예측하는 기본적인 알고리즘이다.
[ KNN 알고리즘의 과정 ]
- 예측해야 할 데이터(x_val)와 주어진 데이터(x_train)들의 모든 거리를 계산한다.
- 가까운 거리의 데이터를 K개(x_train) 만큼 찾는다.
- (회귀의 경우) K개 값의 label 값의 평균을 계산하여 예측한다.
- (분류의 경우) K개 값의 label 값의 범주값을 보고 예측한다.
회귀(Regression)문제 일때와 분류(Classification)문제 일때의 KNN을 그림으로 그려보았다.

[ KNN 알고리즘의 장단점 ]
장점
- 데이터의 분포 형태와 상관이 없다.
- 설명변수(x)의 개수가 많아도 무리 없이 사용 가능
단점
- 계산시간이 오래 걸림
- 훈련데이터를 모델에 함께 저장하기 때문에 모델의 사이즈가 커짐
- 해석하기 어려움
KNN 알고리즘은 K값을 몇으로 설정해주는지에 따라 예측 결과가 달라진다.
K값이 최대일 경우에는 전체 train의 개수과 K값이 같을 것이다. 회귀 모델을 기준으로 한다면 전체 train 데이터의 평균을 구하는 것과 같이 때문에 평균 모델과 같은 의미가 된다.
[ KNN 알고리즘의 거리 계산법 ]
- Euclidean Distance (유클리드 거리)
- Manhattan Distance (맨하탄 거리)
유클리드 거리계산법은 피타고라스의 정리를 이용해 두 지점의 최단거리를 구하는 계산법이다.
맨해튼 거리계산법은 x와 y좌표끼리의 차이의 절댓값을 더해주는 거리 계산법이다.
기본적으로 KNN과 같기 거리를 계산하여 예측하는 알고리즘들은 스케일링을 해주어야 한다.
스케일링(Scaling)이란 모든 변수들의 값의 범위를 맞춰주는 것을 만한다.
feature들 값의 범위와 단위가 각각 다르면 값의 범위가 큰 feature일수록 거리 계산에 영향을 많이 줄 수 있기 때문에 스케일링은 반드시 해주어야 한다.
[ Scaling 대표적인 방법 ]
- Normalization : 모든 값을 0~1로 (최소값:0, 최대값:1)
- Standardization : 평균은 0, 표준편차는 1로
KNN 알고리즘은 K값과 거리계산법에 따라 성능이 달라지기 때문에 여러 방식으로 파라미터를 조절하면서 최적의 모델을 찾아내는 것이 중요하다.
[ 데이터 스케일링 코드 ]
Normalization
- MinMaxScaler() 사용
- fit_transform() : 기준을 찾아내고, 기준에 맞춰 변수에 스케일링을 적용시켜준다.
- transform() : 스케일링 적용
# Normalization 스케일링
from sklearn.preprocessing import MinMaxScaler # 모든 값을 0~1 사이로
scaler = MinMaxScaler() # 선언
x_train_s1 = scaler.fit_transform(x_train) # fit_transform : fit(기준 찾아줌) + transform(계산) = 기준(각 칼럼의 min,max값)을 찾고 적용
x_val_s1 = scaler.transform(x_val) # 적용만
Standardization
- StandarScaler() 사용
# Standardization 스케일링
from sklearn.preprocessing import StandardScaler # 평균:0, 표준편차:1로
scaler2 = StandardScaler()
x_train_s2 = scaler2.fit_transform(x_train) # 원래 값의 평균과 표준편차를 찾고 적용
x_val_s2 = scaler2.transform(x_val)
[ KNN 모델링 코드 ]
- 모델 및 모델평가 메서드 불러오기
# 모델링용
from sklearn.neighbors import KNeighborsRegressor
# 회귀모델 평가용
from sklearn.metrics import * # *는 다불러옴
- 모델선언, 학습, 예측
- KNeighborRegressor() : KNN의 회귀 알고리즘 모델을 선언
- KNeighborsClassifier() : KNN의 분류 알고리즘 모델을 선언
- 하이퍼파라미터 옵션
- n_neighbors = 10 : K의 개수를 지정 (디폴트 값 : K=5)
- metric='manhattan' : 거리계산 방법을 지정 (디폴트값 : 'euclidean')
model = KNeighborsRegressor() # k 디폴트값 : 5
model.fit(x_train_s1, y_train)
pred = model.predict(x_val_s1)
- 모델 평가
실습 코드는 회귀문제이기 때문에 이전 시간에 배운 RMSE, MAE, MAPE값을 구해준다.
# RMSE
mean_squared_error(y_val, pred, squared=False)
# 4.227564933050456
# MAE
mean_absolute_error(y_val, pred)
# 3.035
# MAPE : 평균 오차율
mean_absolute_percentage_error(y_val, pred)
# 0.16339021011462934
2. Logistic Regression (로지스틱 회귀)
로지스틱 회귀는 이름에 회귀가 들어가 있지만 선형회귀와 다르게 분류 문제만 풀 수 있는 알고리즘인데, 분류 문제 중에서도 답이 두가지 범주(ex - 0과1)인 이진분류 문제만 풀 수 있다.
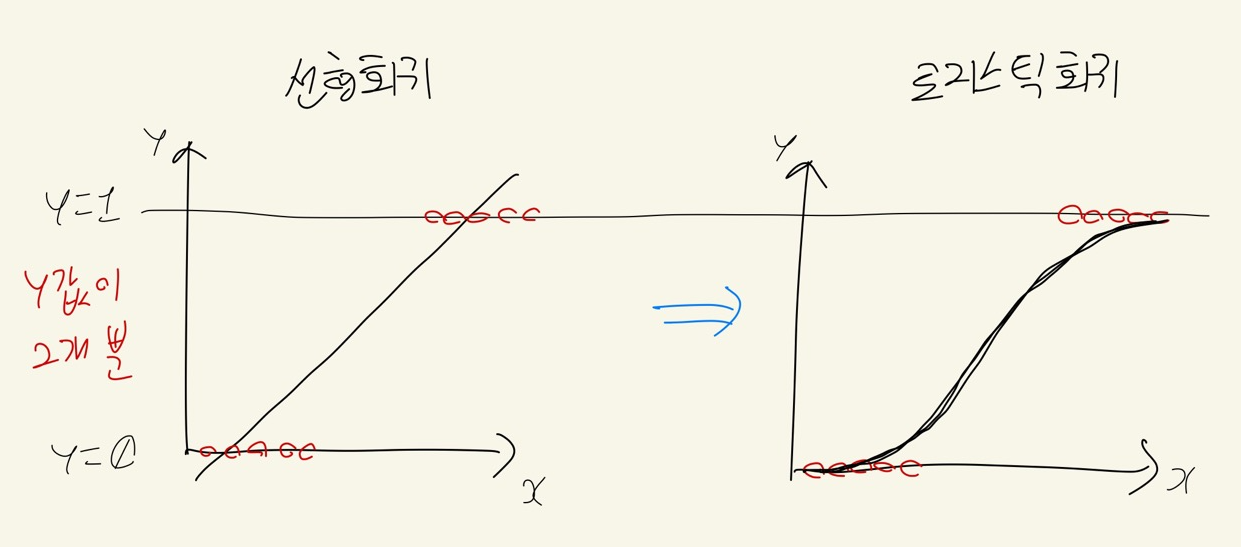
아래 그림과 같이 y의 값이 0과 1뿐인 이진분류 문제일 때,
선형회귀식f(x)으로 그래프를 그려주면 y값은 0과 1 두개 뿐임에도, f(x)의 범위는 음의 무한대~양의 무한대가 돼버린다.
따라서 이 범위를 0~1로 변환해 주는 것이 로지스틱 회귀 알고리즘이다.
로지스틱 함수 식은 다음과 같으며, 시그모이드 함수라고도 한다.
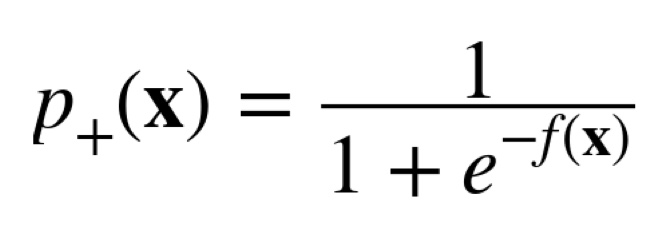
-f(x)는 선형회귀식이다.
로지스틱 회귀식에서의 회귀계수를 해석할 때
- 회귀계수 - : 0에 가까워짐
- 회귀계수 + : 1에 가까워짐
으로 해석할 수 있다.
로지스틱 회귀의 성능을 변화시키는 요인에는 변수가 있다.
따라서 변수 선택이 중요하며, 여러 변수 조합을 시도해보면서 최적의 모델을 찾아내는 것이 중요하다.
[ 로지스틱 회귀 모델링 코드 ]
- 모델 및 모델평가 함수 불러오기
- LogisticRegression() 사용
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import *
- 모델 선언, 학습, 예측
model = LogisticRegression()
model.fit(x_train, y_train)
pred = model.predict(x_val)
- 모델의 회귀계수 확인
print(list(x_train)) # 칼럼 이름을 리스트로 보기
# ['Age', 'DistanceFromHome', 'MonthlyIncome', 'PercentSalaryHike', 'TotalWorkingYears', 'Gender_Male', 'JobSatisfaction_2', 'JobSatisfaction_3', 'JobSatisfaction_4', 'MaritalStatus_Married', 'MaritalStatus_Single', 'OverTime_Yes']
# 회귀계수 확인
print(model.coef_)
# [[-3.84351776e-02 3.84109660e-02 -7.07163728e-05 -2.82800745e-02
# -3.93205061e-02 2.30389163e-01 -2.18808054e-01 -1.05153540e-01
# -3.11618983e-01 -4.12369946e-01 8.41629589e-01 1.26840274e+00]]
위의 데이터는 IBM의 직원 이직률 데이터로 위의 회귀계수를 바탕으로 몇 가지 변수에 대해 모델 해석을 해보면 다음과 같다. (이직: 1, 잔류: 0)
- Age : 나이 많을수록 잔류
- DistanceFromHome : 거리 멀 수록 이직
- MonthlyIncome : 돈을 많이 받을수록 잔류
- PercentSalaryHike : 임금 인상률이 높을수록 잔류
- ...등등
3. 분류 모델의 평가 방법
분류 모델을 평가할 때에는 Confusion Matrix 라는 행렬을 평가 지표로 활용한다.

confusion matrix의 행은 실제값 y를 나타내고, 열은 예측값 y^를 나타낸다.
confusion matrix를 사용해서 우리는 4가지의 성능지표를 활용한다.
- Accuracy (정분류율) : 전체 중에서 맞춘 비율
- Recall (재현율) : 실제 해당 class 중에서 맞춘 비율
- Precision (정밀도) : 해당 class라고 예측한 것 중 맞은 비율
- F1 Score : Recall과 Precision의 조화평균
이 중에서 Accuracy(정분류율)은 전체 관점에서의 성능지표이고, 나머지 3가지는 0 혹은 1의 특정 관점에서의 성능지표를 나타낸다.
위에서 사용했던 IBM 직원의 이직률 데이터의 로지스틱 회귀 모델을 직접 평가해보자
confusion_matrix()를 사용해서 confusion matrix를 확인해준다.
confusion_matrix( y_val , pred )
# array([[293, 7],
# [ 45, 14]], dtype=int64)위의 결과로 이직한 경우(1)를 14개 맞추었고, 이직하지 않은 경우(0)를 293개 맞추었다는 것을 알 수 있다.
classification_report() 를 통해서 우리는 분류문제의 평가지표를 종합적으로 한번에 확인이 가능하다.
print(classification_report(y_val , pred ))
# precision recall f1-score support
# 0 0.87 0.98 0.92 300
# 1 0.67 0.24 0.35 59
# accuracy 0.86 359
# macro avg 0.77 0.61 0.63 359
# weighted avg 0.83 0.86 0.83 359classification_report()를 사용해서 바로 accuracy값과 0과 1 각각에 대한 precision, recall, f1-score 값들을 한눈에 볼 수 있다.
위의 성능지표 값들을 각각 확인해 보는 함수들도 존재한다.
- Accuracy (정분류율) --> accuracy_score( 실제값, 예측값 )
- Precision (정밀도) --> precision_score( 실제값, 예측값, pos_label = 1 )
- Recall (재현율) --> recall_score( 실제값, 예측값, pos_label = 1 )
- F1 Score --> f1_score( 실제값, 예측값, pos_label = 1 )
from sklearn.metrics import *
# 정분류율
accuracy_score(y_val, pred)
# 0.8551532033426184
# 정밀도 (pos_label 옵션 디폴트는 1)
print(precision_score(y_val, pred, pos_label = 0))
print(precision_score(y_val, pred, pos_label = 1))
# 0.8668639053254438
# 0.6666666666666666
# 재현율
print(recall_score(y_val, pred, pos_label = 0))
print(recall_score(y_val, pred, pos_label = 1))
# 0.9766666666666667
# 0.23728813559322035
# f1_score
print(f1_score(y_val, pred, pos_label = 0))
print(f1_score(y_val, pred, pos_label = 1))
# 0.9184952978056425
# 0.35
'KT AIVLE School' 카테고리의 다른 글
| (5주차 - 22.08.25) 머신러닝4 - 모델 성능 향상, 앙상블 (0) | 2022.08.26 |
|---|---|
| (5주차 - 22.08.24) 머신러닝3 - 결정트리,SVM,모델성능튜닝 (0) | 2022.08.25 |
| (5주차 - 22.08.22) 머신러닝1 - 선형회귀,회귀모델평가 (0) | 2022.08.22 |
| (4주차 - 22.08.16~22.08.19) 미니프로젝트1 (0) | 2022.08.22 |
| (3주차 - 22.08.12) 데이터 분석 및 의미 찾기 3 - 이변량분석2 (2) | 2022.08.15 |
