[ 오늘 배운 내용 ]
1. Decision Tree (결정 트리)
- 트리 알고리즘이란
- 지니 불순도, 정보 증가량
- 모델링
- 하이퍼파라미터 : max_depth, min_samples_leaf
- 의사결정나무 모델 시각화
2. Support Vector Machine (SVM)
- SVM이란
- 결정 경계, 서포트 벡터, 마진
- 하이퍼파라미터 : Cost(비용), Gamma
3. 성능 튜닝 방법
- 선형 모델 : 변수 선택법
- 전진선택법 (후진선택법)
- AIC (아카이케 통계량)
- 하이퍼파라미터 튜닝
- Random Search
- Grid Search
1. Decision Tree (결정 트리)
Tree 기반 알고리즘은 특정 항목(변수)에 대한 의사 결정(분류) 규칙을 나무의 가지가 뻗는 형태로 분류해 나가는 분석 기법이다. 자료구조의 트리와 같은 구조를 생각하면 된다.
트리 기반 알고리즘은 분석 과정이 직관적이고 이해하기 쉬우며, 계상 비용이 낮아 대규모의 데이터셋에서도 빠른 비교적 빠른 연산이 가능하다.
Decision tree 알고리즘은 분류와 회귀 문제 모두에서 사용이 가능하다.
Decision tree 알고리즘 에서는 타겟 변수에 대해서 어떤 속성이 중요한 정보를 담고 있는지를 알아낸 뒤, 해당 속성을 기준으로 가지를 뻗어야 한다.
이 때 중요한 정보를 담고 있는 속성을 찾아내는 기준으로 불순도를 사용한다.
결정 트리 알고리즘에서 불순도는 지니 불순도 (Gini Impurity)라는 지표를 통해 측정할 수 있다.
각 변수의 지니 불순도는 해당 변수값들 각각의 지니 계수들의 가중평균을 통해 구해줄 수 있다. 코드 작성 시 알아야 하는 부분은 아니라서 따로 정리하지는 않았다.
이 때 [부모의 불순도 - 자식의 불순도]를 구해준 값을 Information gain (정보증가량, 정보전달량)이라고 하는데 이는 부모의 불순도를 해당 변수가 얼마나 떨어트려 줬는지를 의미하는 지표이다. Information gain을 통해 우리는 어떤 속성이 얼마나 많은 정보를 제공해주는지를 알 수 있다.
결정 트리에서 가지를 뻗어나갈 때는 각 변수마다의 Information gain값을 구해주고, 이 값이 가장 큰 변수 즉, 부모의 불순도를 가장 많이 떨어뜨려준 변수를 골라서 해당 변수를 기준으로 split해준다.
결정 트리 모델은 트리의 크기(max_depth)에 따라 예측 결과(정확도)가 달라진다.
트리 모델이 다 만들어진 뒤, 검증 데이터가 만들어진 결정 트리 안에서 해당하는 방향으로 말단까지 내려왔을 때, 마지막으로 도착한 노드에 담겨있는 train 데이터들을 바탕으로 결과를 판단한다.
이 때, 트리의 가장 끝에 있는 노드들을 Leaf node 라고 하며, 각 리프노드에는 지정된 수 이상의 train 데이터들이 담겨있다.
결정 트리 모델의 성능을 튜닝할 때는 위에서 설명한 두가지 하이퍼파라미터의 값을 조절해준다.
- max_depth : tree의 경로의 길이
- min_samples_leaf : leaf노드의 최소 데이터 건수 (디폴트1 --> 가장 복잡한 트리)
[ Decision tree 모델링 코드 ]
아래 실습 코드에서는 분류를 수행하는 결정 트리 모델을 DecisionTreeClassifier()를 사용해서 불러왔다.
- 모델 생성, 학습, 예측
# 모델링을 위해
from sklearn.tree import DecisionTreeClassifier
# 평가를 위해.
from sklearn.metrics import *
# 디폴트로 만들면 가장 복잡한 tree가 됨
model = DecisionTreeClassifier()
model.fit(x_train, y_train)
pred = model.predict(x_val)
- 모델 검증(평가)
confusion_matrix(y_val, pred)
# array([[266, 34],
# [ 40, 19]], dtype=int64)
print(classification_report(y_val, pred))
# precision recall f1-score support
#
# 0 0.87 0.89 0.88 300
# 1 0.36 0.32 0.34 59
#
# accuracy 0.79 359
# macro avg 0.61 0.60 0.61 359
# weighted avg 0.79 0.79 0.79 359
하이퍼파라미터 조절
- max_depth : 트리의 깊이(크기를 결정)
- min_samples_leaf : leaf 노드의 최소 데이터 건수
leaf 노드는 y를 예측하는데 사용되는데, 데이터가 적으면 예측 결과에 대해 신뢰도가 떨어질 수 있기 때문에 되도록이면 너무 작은 값은 지양하자.
- max_depth 설정한 뒤 모델링
# max_depth = 2로 설정
model1 = DecisionTreeClassifier(max_depth = 2)
model1.fit(x_train, y_train)
pred1 = model1.predict(x_val)
print(classification_report(y_val, pred1))
# precision recall f1-score support
#
# 0 0.87 0.93 0.90 300
# 1 0.47 0.31 0.37 59
#
# accuracy 0.83 359
# macro avg 0.67 0.62 0.64 359
# weighted avg 0.81 0.83 0.81 359
- min_samples_leaf 설정한 뒤 모델링
# min_samples_leaf = 30으로 설정
model3 = DecisionTreeClassifier(min_samples_leaf = 30)
model3.fit(x_train, y_train)
pred3 = model3.predict(x_val)
print(classification_report(y_val, pred3))
# precision recall f1-score support
#
# 0 0.86 0.96 0.91 300
# 1 0.52 0.22 0.31 59
#
# accuracy 0.84 359
# macro avg 0.69 0.59 0.61 359
# weighted avg 0.81 0.84 0.81 359
[ 결정 트리 모델 시각화 ]
plot_tree()를 사용해서 시각화를 통해 결정 트리 모델의 내부를 들여다 볼 수 있다.
# 시각화
from sklearn.tree import plot_tree
# Decision Tree모델 시각화
plt.figure(figsize = (20,10)) # 그림 사이즈 조절
plot_tree(model1, feature_names = list(x_train),
class_names= ['Stay', 'Leave'], filled = True, fontsize = 20);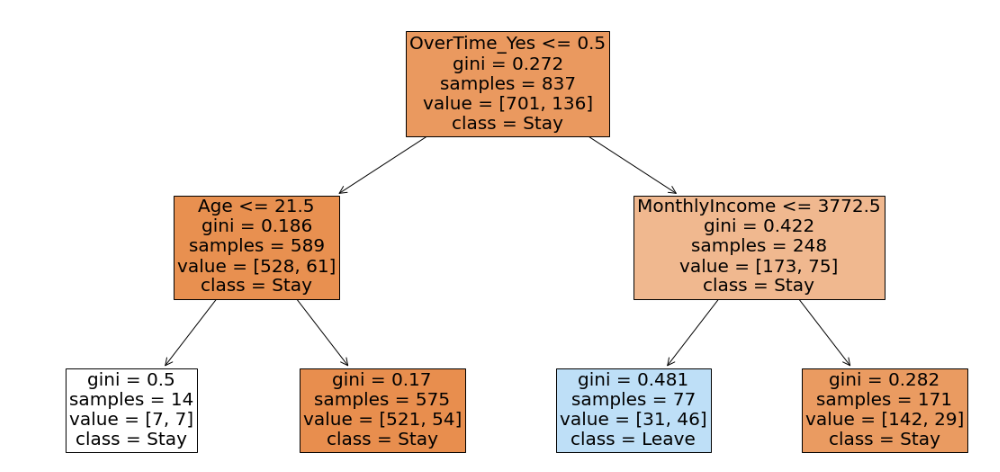
root 노드를 기준으로 시각화 내용을 설명하자면
- OverTime_Yes <= 0.5
: 'OverTime_Yes' 변수가 Information gain이 가장 높은 변수(부모의 불순도를 가장 떨어뜨려주는)임. 따라서 아래로 뻗어나가는 가지들은 OverTime_Yes 값이 0인지 1인지로 갈린다.
- gini = 0.272
: 지니불순도 값 = 0.272
- samples = 837
: train 데이터 크기 (837개)
- value = [701, 136]
: Stay(0) 값이 701개, Leave(1) 값이 136개
- class = Stay
: 해당 노드에서는 Stay라고 판단
- 변수 중요도 확인하기
트리 알고리즘에서는 변수 중요도 라는 지표를 제공한다.
변수 중요도는 해당 트리에서 가장 중요하게 사용되는 변수를 확인할 수 있는 지표로 모델.feature_importances_ 를 사용해서 각 변수의 중요도를 확인할 수 있다.
# 변수 중요도
print(list(x_train))
print(model.feature_importances_)
# ['Age', 'DistanceFromHome', 'MonthlyIncome', 'PercentSalaryHike', 'TotalWorkingYears', 'Gender_Male', 'JobSatisfaction_2', 'JobSatisfaction_3', 'JobSatisfaction_4', 'MaritalStatus_Married', 'MaritalStatus_Single', 'OverTime_Yes']
# [0.17967734 0.13157593 0.28673383 0.06125723 0.14691249 0.02366808
# 0.01766537 0.01365696 0.03633215 0.00774086 0.03419288 0.06058689]
.feature_importances_로 구한 변수 중요도는 전체 트리를 기준으로 사용된 모든 변수들의 각 중요도의 평균을 구한 값이다. 따라서 트리의 맨 위에서 사용된 변수라고 해서 변수 중요도가 가장 높다고 할 수 없다는 점을 참고하자.
2. Support Vector Machine (SVM)
서포트 벡터 머신은 분류와 회귀 문제 모두에서 사용이 가능하다.
분류 모델을 기준으로 설명하자면 서포트 벡터 머신 알고리즘의 기본 아이디어는 두 클래스 사이에 가장 넓은 도로를 내는 것이다.
가장 넓은 도로란 마진을 가장 크게 하는 결정 경계선을 의미한다.
서포트 벡터 머신에서는 다음의 용어들이 중요한 의미를 갖는다.
- 결정 경계 (Decision Bounday) : 클래스를 구분하는 경계선 --> 결정 경계가 SVM 모델이다. (초평면-hyper plane이라고도 함)
- 벡터 (Vector) : 모든 데이터 포인트
- 서포트 벡터 (Support Vector) : 결정 경계와 가까운 데이터 포인트 -> 서포트 벡터를 찾는 것이 SVM 알고리즘의 목적
- 마진 : 서포트벡터와 결정경계 사이의 거리. (도로의 폭)
아래의 두 SVM 모델을 비교해보자
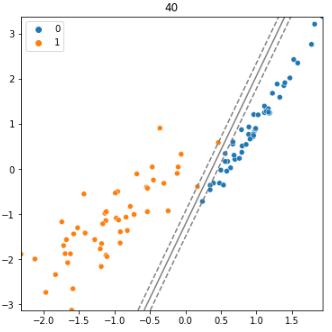
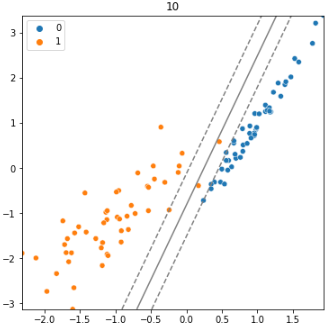
왼쪽 모델의 경우에는 하나의 오차도 허용하지 않고 완벽하게 분류를 수행한다.
하지만 마진이 좁기 때문에 조금만 데이터가 벗어나도 잘못 분류될 가능성이 높다.
반면에 오른쪽 모델은 몇개의 오차를 허용하는 것을 볼 수 있다.
하지만 마진이 넓기 때문에 기존 데이터에서 조금 벗어나도 안정적으로 제대로 된 값으로 분류가 가능하다.
위의 예시만 봐도 알 수 있듯이 모델을 완벽하게 만드는 것이 무조건 좋은 게 아니다.
따라서 우리는 다양하게 하이퍼파라미터 값들을 튜닝해가면서 완벽한 모델이 아닌, 가장 적절한 모델을 찾아내야 한다.
SVM은 다음의 두가지를 달성하는 것을 목적으로 한다.
- 마진(도로의 폭)은 가능한 넓게
- 오류는 가능한 적게
하지만 위의 두 사항은 서로 상반되는 조건이기 때문에 우리는 마진의 크기와 오류에 대한 허용 정도의 최적의 조합을 찾아야 한다. SVM 모델에 .fit()을 적용해줄 때 이 작업이 수행되는 것이다.
여기서 우리가 인위적으로 조절할 수 있는 파라미터는 C(비용)이다.
이는 오류에 대한 허용 정도를 뜻하며, 학습 시 Train set의 오류를 허용하지 않으려는 비용이라고 이해하면 되겠다.
- C 값을 높이면 : 오류를 허용하지 않으려는 비용 증가 --> 오버피팅(Overfitting) 가능성이 높아짐
- C 값을 낮추면 : 오류를 허용하지 않으려는 비용 감소 --> 언더피팅(Underfitting) 가능성이 높아짐
근데 지금까지의 설명들은 선형적으로 분류할 수 있는 데이터의 경우라면 이해가 잘 되겠지만 현실적으로는 여러개의 feature를 갖기 때문에 선형적으로 분류할 수 없는 데이터셋이 훨씬 많을 것이다.
하지만 SVM은 직선 혹은 초평면으로 분류하는 방식의 선형 분류기이다. SVM은 커널 트릭(Kernel Trick)이라는 기법을 사용해서 실제 고차원 feature를 생성하지 않고도, 추가한 것과 같은 효과를 얻도록 해준다.
쉽게 풀어 말하면 직선(평면으로) 데이터가 분류 되도록 고차원으로 데이터의 배치만 변형해준다고 생각하면 될 것 같다.
커널의 종류에는 poly, rbf, sigmoid 등이 있고, 모델 생성 시 옵션으로 이를 지정해 줄 수 있는데 대부분의 경우에 디폴트값인 rbf를 쓴다.
[ SVM 모델 코드 작성 ]
SVM 알고리즘은 값들과의 길이를 조절하며 모델을 만들기 때문에 스케일링을 해주어야 한다.
# 변수 스케일링
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
x_train = scaler.fit_transform(x_train)
x_val = scaler.transform(x_val)
- 모델 불러오기, 선언, 학습, 예측
# SVC: 분류, SVR: 회귀
from sklearn.svm import SVC
# 평가용
from sklearn.metrics import *
model = SVC()
model.fit(x_train, y_train)
pred = model.predict(x_val)
- 모델 검증(평가)
confusion_matrix(y_val, pred)
# array([[436, 295],
# [204, 565]], dtype=int64)
print(classification_report(y_val, pred))
# precision recall f1-score support
#
# LEAVE 0.68 0.60 0.64 731
# STAY 0.66 0.73 0.69 769
#
# accuracy 0.67 1500
# macro avg 0.67 0.67 0.66 1500
# weighted avg 0.67 0.67 0.67 1500
SVM 모델에서는 다음의 두가지 하이퍼파라미터를 조절하여 성능 튜닝을 할 수 있다.
- C (cost) : 오류를 허용하지 않으려는 비용. 값이 클 수록 마진폭이 줄어들고, 오류를 허용하지 않기 위한 경계를 만든다.
- gamma : 결정경계의 곡률. 값이 클 수록 곡률반경이 작아져서 촘촘한 모델이 만들어진다.
공통적으로 C와 gamma 값 모두 커질수록 모델은 복잡해진다.
- C값에 따른 경계 확인해보기
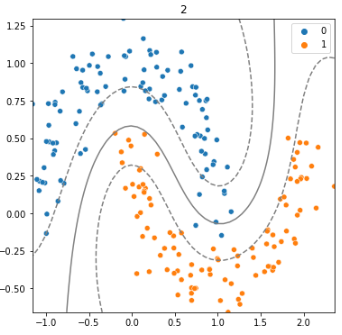
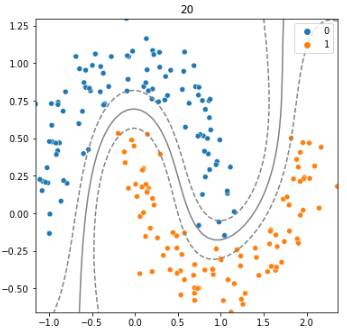
왼쪽은 C=2, 오른쪽은 C=20일때의 SVM 모델을 시각화한것이다.
C값이 클수록 오류를 허용하지 않으려는 비용이 많아지고, 마진의 폭이 줄어든다.
- gamma값에 따른 경계 확인해보기
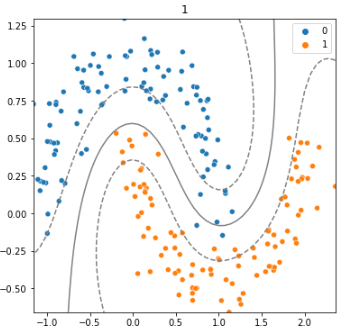
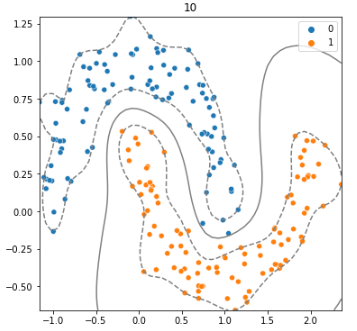
왼쪽은 gamma=1, 오른쪽은 gamma=10일때의 SVM 모델을 시각화한것이다.
gamma값이 클수록 곡률반경이 작아지고 모델이 복잡해지는 것을 볼 수 있다.
참고로 높은 차원의 SVM 모델의 시각화는 할 수 없기 때문에 위의 그림들은 임의로 만든 함수를 통해 확인해본 것이다.
따라서 실제 SVM 모델의 성능평가는 C와 gamma값 별 모델의 예측 결과를 가지고 accuracy, percision, recall, f1_score 등의 분류모델 평가지표를 활용해주도록 하자.
3. 성능 튜닝 방법
지금까지 회귀, 분류 문제들을 풀기 위한 여러가지 알고리즘들을 공부했다.
이 알고리즘들의 성능을 튜닝하려면
- 선형 모델(선형 회귀, 로지스틱 회귀)의 경우에는 좋은 성능을 낼 수 있는 가장 적절한 변수 조합을 찾아내기 위해 변수 선택을 해주는 것이 좋다.
- KNN, Decision Tree, SVM 등의 모델은 하이퍼파라미터의 값을 조절하여 좋은 성능을 낼 수 있는 가장 적절한 조합을 찾아주는 방식을 주로 사용한다.
[ 선형 모델 - 변수 선택법 ]
선형회귀, 로지스틱 회귀와 같은 선형모델의 성능은 변수 선택에 따라 차이가 많이 발생된다.
모든 feature 변수를 사용하게 되면 모델이 복잡해진다. 따라서 target에 영향을 많이 주는 몇개의 변수(feature)들만 학습에 사용하는 것이 더 좋을 수도 있다.
변수를 선택하는 방법에는 전진선택법(후진소거법)이 있다.
전진선택법의 과정은 AIC 값이 가장 작은 변수 조합의 모델을 단계별, 순차적으로 탐색하는 것으로 다음과 같다.
- Step1. feature별로 각각 단순회귀 모델을 생성하고 AIC값을 비교하여 제일 작은 변수(feature) 선정
- Step2. Step1에서 선정된 변수에 이어서 나머지 변수를 하나씩 추가해가며 AIC값이 가장 작은 모델의 변수를 선정해준 다. (단, 이전 단계보다 AIC가 더 낮아져야 한다.)
- Step3. 더 이상 AIC가 낮아지지 않을 때까지 Step2를 반복한다.
후진소거법은 전진선택법의 반대로 진행한다.
참고로 AIC값이란 Akaike Information Criterion의 약자로 아카이케 통계량 이라고 하는 값이다.
모델이 학습 데이터셋을 얼마나 잘 설명하는지는 매우 중요하지만 모델이 과적합 되지 않도록 하는 것도 중요하다. 그래서 선형 모델에서의 적합도와 feature가 과도하게 늘어나는 것을 방지하도록 설계된 통계량이 AIC인데,
결론적으로는 AIC값이 작을수록 좋은 모델이라는 것만 기억하자.
===> 우리의 목적은 적절한 성능 + 적절한 복잡도의 모델을 찾는 것
[ 하이퍼파라미터 튜닝 ]
이전에 배운 KNN, Decision tree, SVM 등의 알고리즘들은 변수 선택이 아닌 하이퍼파라미터 튜닝을 통해서 성능이 달라질 수 있다.
하이퍼파라미터란 기계가 학습할 때 사람이 개입해주는 부분으로 모델링 시에 직접 값을 지정해주어야 하는 파라미터 들을 말한다.
KNN, Decision tree, SVM 모델의 경우 대표적으로 다음과 같은 하이퍼파라미터들을 튜닝해줄 수 있다.
- KNN : K값(n_neighbors), 거리계산법(metric)
- Decision tree(결정트리) : 트리의 최대깊이(max_depth), 리프 노드의 최소 데이터 건수(min_samples_leaf)
- SVM : 오차를 줄이기 위한 비용(C), 모델이 생성하는 경계가 복잡해지는 정도(gamma)
하이퍼파라미터를 튜닝하는 방법에는 정답이 없다. 지식과 경험, 그리고 다양한 시도를 통해서 가장 적절한 조합을 찾을 줄 알아야 하며,
여러 하이퍼파라미터의 조합을 탐색해보기 위한 방법은 다음의 두 가지가 있다.
- Grid Search (그리드 서치)
- Random Search (랜덤 서치)
[ Grid Search vs Random Search ]
Grid Search와 Random Search 모두 지정된 하이퍼파라미터 값의 범위 내에서 여러 시도를 해보는 방식인데 조금씩 차이가 있다.
Grid Search의 과정
- 값의 범위를 지정한다.
- 값의 조합을 모두 시도한다.
- 가장 성능이 좋은 값을 선정한다.
Random Search의 과정
- 값의 범위를 지정한다.
- 시도 횟수를 지정한다.
- 값의 범위 내에서 시도 횟수만큼 랜덤하게 선택해서 시도한다.
- 가장 성능이 좋은 값을 선정한다.
[ Random Search 코드 작성 실습]
먼저 sklearn.model_selection 모듈의 RandomizedSearchCV를 임포트 해주고 값의 범위를 지정한 하이퍼파라미터를 딕셔너리의 형태로 선언해준다. 지정하지 않은 하이퍼파라미터는 기본값으로 지정된다.
아래 코드는 KNN 분류 모델을 기준으로 작성하였고, n_neighbors와 metrics와 같이 실제 하이퍼파라미터 옵션의 이름과 똑같이 딕셔너리의 키값을 지정해주어야 한다.
from sklearn.model_selection import RandomizedSearchCV
# 값의 범위 지정 - dictionary형태로 선언
params = { 'n_neighbors' : range(1,51), 'metric' : ['euclidean', 'manhattan'] }
params
# {'n_neighbors': range(1, 51), 'metric': ['euclidean', 'manhattan']}
그다음 모델을 선언해주는데 그냥 모델을 먼저 선언해준 뒤, 선언한 모델을 사용해서 RandomizedSearchCV() 모델을 다시 선언해준다.
그 다음 기본 모델이 아닌 RandomizedSearchCV() 모델에 .fit()으로 학습을 시켜준다.
# 기본모델
model = KNeighborsClassifier()
# Random Search 설정.
model_rs = RandomizedSearchCV(model
, params # hyperparameter 범위 지정.
, cv=5 # k-fold Cross Validation
, n_iter=5 # Random하게 시도할 횟수
)
# 학습 : model이 아니라 model_rs에
model_rs.fit(x_train_s, y_train)
# RandomizedSearchCV(cv=5, estimator=KNeighborsClassifier(), n_iter=5,
# param_distributions={'metric': ['euclidean', 'manhattan'],
# 'n_neighbors': range(1, 51)})n_iter는 랜덤하게 시도할 횟수를 지정해주는 옵션이다.
튜닝의 결과는 모델.cv_results_ 를 사용해서 딕셔너리 형태로 확인이 가능하다.
우리는 여기서 mean_test_score와 params만 확인해주면 된다.
- mean_test_score : 랜덤하게 시도한 모델들의 성능
- params : 랜덤하게 시도했을 때의 하이퍼파라미터값들
# 튜닝 결과
model_rs.cv_results_
참고로 mean_test_score는 회귀에서는 R2 score, 분류에서는 accuracy 값을 나타낸다. (평가 지표를 다른 값으로 변경도 가능하다.)
모델.best_params_ 와 모델.best_score_ 을 사용해서 최적의 파라미터와 그 때의 성능도 바로 확인이 가능하다.
# 최적의 파라미터
model_rs.best_params_
# {'n_neighbors': 36, 'metric': 'manhattan'}
# 그때의 성능
model_rs.best_score_
# 0.6222857142857143
랜덤서치 모델을 학습시키고 예측과 평가를 할 때는 기존의 예측 코드와 똑같이 작성해주면 모델이 얻어낸 모델 중 최적의 파라미터를 가진 모델로 알아서 예측 및 평가를 수행해준다.
# best 모델로 알아서 예측 및 평가
pred = model_rs.predict(x_val_s)
print(classification_report(y_val, pred))
# precision recall f1-score support
#
# 0 0.59 0.78 0.67 738
# 1 0.69 0.47 0.56 762
#
# accuracy 0.62 1500
# macro avg 0.64 0.62 0.61 1500
# weighted avg 0.64 0.62 0.61 1500
[ Grid Search 코드 작성 실습]
그리드 서치 시에는 sklearn.model_selection 모듈의 GridSearchCV를 임포트 해주어야 하고 n_iter를 지정해주지 않는 것만 빼면 랜덤서치와 거의 동일하다.
- 함수 불러오기 & 하이퍼파라미터 값 범위 지정
from sklearn.model_selection import GridSearchCV
# 값의 범위 지정
params = { 'n_neighbors' : range(3,31,2), 'metric' : ['euclidean', 'manhattan'] }
params
# {'n_neighbors': range(3, 31, 2), 'metric': ['euclidean', 'manhattan']}
- 모델 선언, 학습
# 기본모델
model = KNeighborsClassifier()
# Random Search 설정.
model_gs = GridSearchCV(model, params, cv=5)
# 학습 : model이 아니라 model_rs
model_gs.fit(x_train_s, y_train)
# GridSearchCV(cv=5, estimator=KNeighborsClassifier(),
# param_grid={'metric': ['euclidean', 'manhattan'],
# 'n_neighbors': range(3, 31, 2)})옵션에 넣어준 cv=5의 의미는 5-Fold Cross Validation을 수행한다는 의미인데 이는 다음 글에서 정리하도록 하겠다.
간단하게 말하면 모델링 시, 모델의 성능을 평가하기 위해 해당 모델을 여러번 반복실행 한 뒤 평균을 낸 성능을 사용하는데, 이 때 여러번 시도할 때 데이터를 cv=로 지정해준 숫자만큼 등분해준 뒤 한번씩 validation용으로 사용하여 평가하는 방법이다.
- 결과 확인
# 튜닝 결과 확인 (랜덤서치와 동일)
model_gs.cv_results_
# 최적의 파라미터
model_gs.best_params_
# {'metric': 'manhattan', 'n_neighbors': 27}
# 그때의 성능
model_gs.best_score_
# 0.6185714285714285
- 예측 및 평가
# best 모델로 예측 및 평가
pred = model_gs.predict(x_val_s)
print(classification_report(y_val, pred))
# precision recall f1-score support
#
# 0 0.59 0.72 0.65 738
# 1 0.65 0.51 0.57 762
#
# accuracy 0.61 1500
# macro avg 0.62 0.61 0.61 1500
# weighted avg 0.62 0.61 0.61 1500
참고로 classification_report로 확인한 accuracy 값과 .best_score로 확인한 값이 다르다는 것을 알 수 있는데,
이는 .fit() 수행 시 하이퍼파라미터 값을 조정하면서 모델을 만들고 검증하는 과정에서 만들어진 모델 중 가장 좋은 성능의 모델이 x_train 데이터셋을 사용했을 때의 점수가 .best_score이고,
accuracy는 선정된 최고성능의 모델에 x_val 데이터셋을 사용하여 예측한 것에 대한 점수이기 때문이다.
모델을 튜닝했을 때 최고 성능을 가진 모델을 따로 확인하고 싶다면 .best_estimator_를 사용해준다.
트리 모델의 경우 시각화와 변수 중요도를 확인할 때 아래와 같이 .best_estimator_로 최적의 모델을 따로 불러와서 사용해야 한다.
아래 코드는 의사결정트리 모델을 그리드 서치로 튜닝한 모델에서 최적의 모델을 갖고와서 시각화와 변수 중요도를 확인해 보는 내용이다.
# 최적의 모델은 아래와 같은 이름을 갖게 된다.
model_tree_gs.best_estimator_
# DecisionTreeClassifier(max_depth=3, min_samples_leaf=80)- 시각화 : plot_tree()
# 그리드서치, 랜덤서치한 모델을 시각화 하려면 .best_estimator_로 최적의 모델을 따로 빼와서 사용해야 한다.
plt.figure(figsize = (20,10)) # 그림 사이즈 조절
plot_tree(model_tree_gs.best_estimator_, feature_names = list(x_train),
class_names= ['Bad', 'Good'], filled = True, fontsize = 20);
- 변수 중요도 확인 : .feature_importances_
# 튜닝한 모델의 변수 중요도 확인
model_tree_gs.best_estimator_.feature_importances_
# array([0.21737046, 0. , 0.0803409 , 0. , 0. ,
# 0. , 0.00535948, 0. , 0. , 0. ,
# 0. , 0. , 0. , 0. , 0. ,
# 0. , 0.69692915, 0. , 0. , 0. ,
# 0. , 0. , 0. , 0. , 0. ,
# 0. , 0. , 0. , 0. , 0. ,
# 0. , 0. , 0. , 0. , 0. ,
# 0. , 0. , 0. , 0. , 0. ,
# 0. ])트리에 사용된 변수들만 중요도가 계산되기 때문에 위와 같은 결과가 나온다.
랜덤서치와 그리드 서치를 배워보았는데 실제로 모델링을 하게 됐을 때, 하이퍼 파라미터 값을 어떻게 정해야 할지 감이 안온다면 랜덤서치와 그리드서치를 함께 사용해주면 좋을 것이다.
먼저 랜덤서치로 임의의 조합들 주 가장 좋은 하이퍼파라미터 조합을 고른 뒤, 그 하이퍼파라미터 주변 범위를 그리드 서치로 조합해본 뒤 그 중 가장 좋은 조합을 찾아내면 좋은 성능의 하이퍼파라미터 조합을 얻어낼 수 있을 것이다.
하지만 파라미터를 너무 세밀하게 조정한다면 주어진 데이터셋에서는 최고의 성능을 얻었을 지라도, 학습에 사용되지 않은 데이터를 다루어야 하는 실제 운영환경에서는 성능이 보장되지 않을 수 있다. 미래에 발생될 데이터는 학습에 사용된 데이터와 다를 수도 있기 때문에 오버피팅의 위험이 있다.
따라서 우리는 완벽한 모델을 찾기보다는 적절한 예측력을 가진 적절한 복잡도의 모델을 얻어내는 것이 중요하다.
'KT AIVLE School' 카테고리의 다른 글
| (5주차 - 22.08.26) 머신러닝5 - 비지도학습 (0) | 2022.08.26 |
|---|---|
| (5주차 - 22.08.25) 머신러닝4 - 모델 성능 향상, 앙상블 (0) | 2022.08.26 |
| (5주차 - 22.08.23) 머신러닝2 - KNN,로지스틱회귀,분류모델평가 (0) | 2022.08.23 |
| (5주차 - 22.08.22) 머신러닝1 - 선형회귀,회귀모델평가 (0) | 2022.08.22 |
| (4주차 - 22.08.16~22.08.19) 미니프로젝트1 (0) | 2022.08.22 |
