[ 오늘 배운 내용 ]
1. 비지도학습
- K-means
- DBSCAN
1. 비지도학습
비지도학습은 지도학습과 다르게 답이 주어지지 않은 문제를 학습하는 것이다.
비지도학습 알고리즘
- K-maens
- DBSCAN
[ K-means ]
K개의 평균으로부터 거리를 계산하고, 가까운 평균으로 묶어서 클러스터(Cluster)를 나누는 방식
클러스터링의 기본이 되는 알고리즘이다.
거리기반 알고리즘이라 스케일링 필요
K-means 절차
- 클러스터의 개수를 지정한다. (구별되는 그룹의 수로 지정하는 것을 권장)
- 그룹의 중심점이 무작위로 선택된다.
- 임의로 선택된 중심점과 각 점 간의 거리를 계산해서 가장 가까운 중심점의 그룹으로 선택된다.
- 선택된 그룹의 점들을 기준으로 중심점을 계산해서 찾는다.
- 3~4를 반복하여 중심점의 변화가 없을 때까지 진행한다.
절차를 그림으로 표현하면 아래와 같은 식이다.
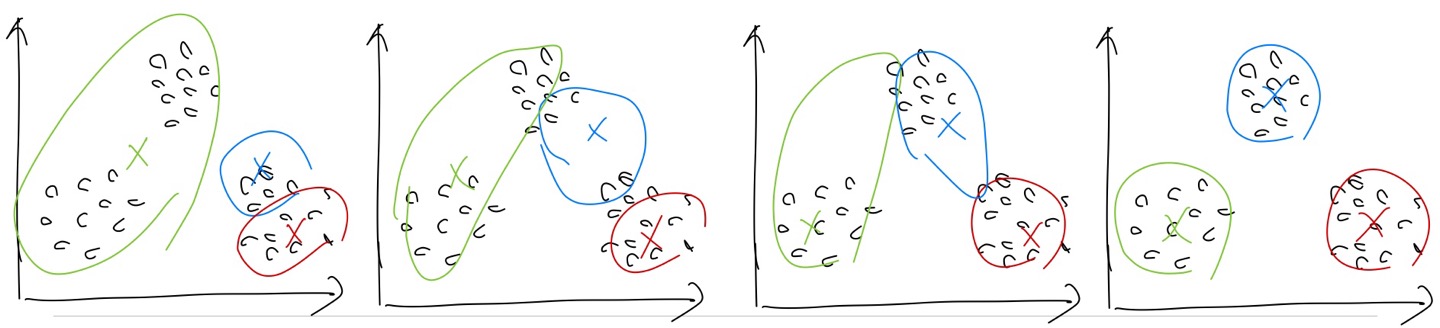
K-means의 장점
- 실행속도가 빠르다.
K-means의 단점
- 최초에 나눌 그룹(클러스터)의 수를 결정해야 한다.
- 무작위로 선정된 중심점에서 시작하다 보니 반복 실행 시 동일한 결과를 얻지 못할 수도 있다.
- 데이터가 덩어리의 형태일 때만 성능 발휘가 가능하다.
아래와 같은 모양의 데이터셋을 활용하여 K-means 코드를 작성해보았다.
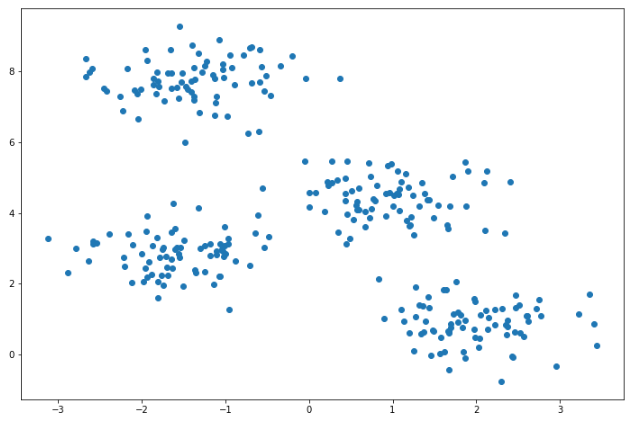
- 모델 불러오기, 학습, 예측
# K-means, DBSCAN 불러오기
from sklearn.cluster import KMeans
# k means 모델 만들고 예측하기
model = KMeans(n_clusters= 2, algorithm='auto') # 군집 2개
model.fit(x) # 비지도학습이라 y가 없기 때문에 .fit()에 x만 넣는다.
pred = model.predict(x)
- 시각화
# k means 모델로 부터 클러스터의 평균 값들 가져오기
centers = pd.DataFrame(model.cluster_centers_, columns=['x1','x2'])
# scatter plot
plt.figure(figsize = (12,8))
plt.scatter(result['x1'],result['x2'],c=result['predicted'],alpha=0.5)
plt.scatter(centers['x1'], centers['x2'], s=50,marker='D',c='r')
plt.show()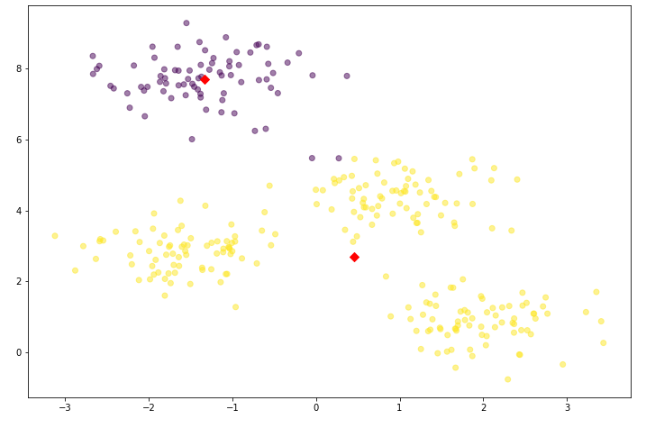
Kmeans()에서 n_clusters=2로 지정했기 때문에 2개의 클러스터로 분류한 것을 볼 수 있다.
n_clusters=4로 지정해주면 아래와 같이 분류한다.
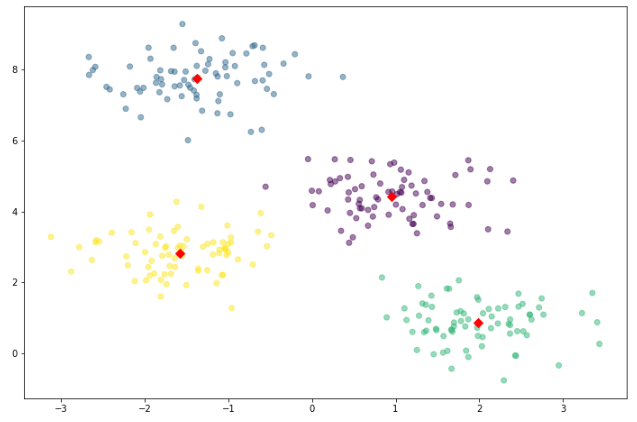
설정해준 K의 값(n_clusters)에 따라 다른 결과가 나오는 것을 볼 수 있다.
클러터의 개수(K)를 지정할 때 데이터의 분포를 눈으로 확인할 수 있다면 몇개로 군집화 할 지 알 수 있다.
하지만 실제로 사용되는 데이터들은 거의 여러 feature를 갖고 있고, 이런 여러 차원의 데이터를 눈으로 보고 군집의 개수를 판단하기 매우 어렵다.
데이터의 분포를 보지 않고 군집의 개수를 고르는 데 참고할 수 있도록 Inertia value라는 값을 사용한다.
Inertia value
: 군집화가 된 후에, 각 중심점에서 군집의 데이터 간의 거리를 합산한 값이다. inertia value 값이 작을 수록 응집도가 높게 군집화가 잘 되었다고 평가한다.
k-means 모델을 생성하게 되면 .inertia_로 inertia 값을 확인할 수 있다.
model.inertia_
# 212.00599621083472
Inertia value의 값을 시각화 해본 뒤 Elbow method로 적정 K값을 찾을 수 있다.
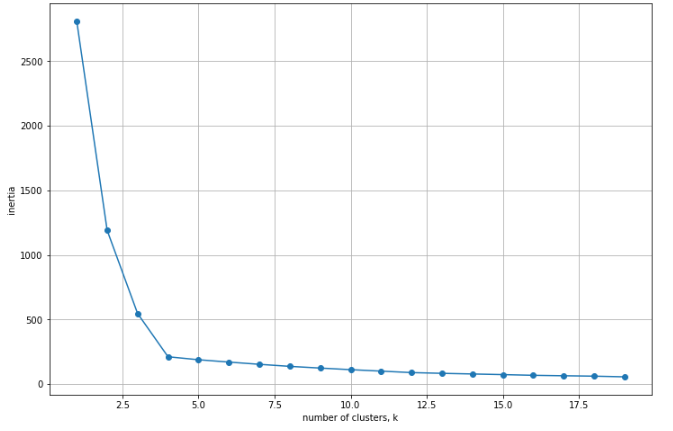
k값 별로 inertia값을 시각화해보았고, k=4 정도가 적절한 지점이라는 것을 판단해볼 수 있다.
Inertia값은 각 중심점에서 군집의 데이터 간의 거리를 합산한 값이기 때문에, inertia값이 작을수록 군집화가 잘 되었다고 평가할 수 있다.
- K=1이면 모든 데이터를 하나의 군집으로 묶어주는 경우이기 때문에 Inertia는 해당 데이터셋에서 얻을 수 있는 가장 큰 값이 나올 것이다.
- K값이 점점 데이터의 수와 가까워지면 Inertia값은 점점 작아지고, K가 데이터의 수 n과 같아지면(K=n) 모든 데이터가 중심점이 되기 때문에 inertia값이 0이 된다
하지만!!!
K-means 모델은 K값을 직접 지정해주어야 한다는 점 말고도 덩어리 형태의 데이터에만 잘 작동한다는 명확한 한계점이 있다.
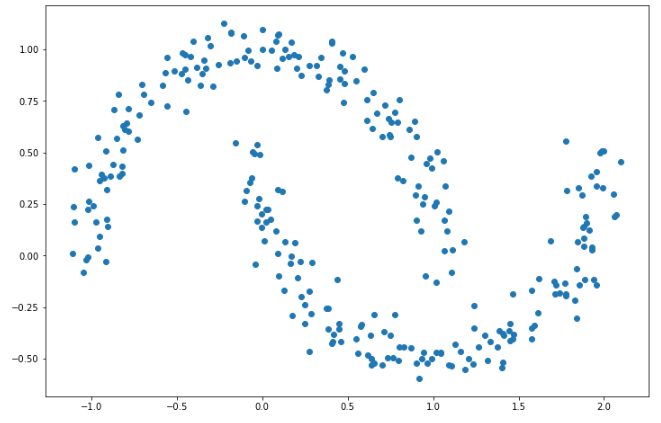
아래와 같은 식의 데이터 분포일 경우, 위아래 초승달 모양의 2가지 군집으로 나누는 것이 가장 좋다.
그러나 K-means로 2개의 군집을 나눠주면 아래와 같은 결과를 얻게 된다.
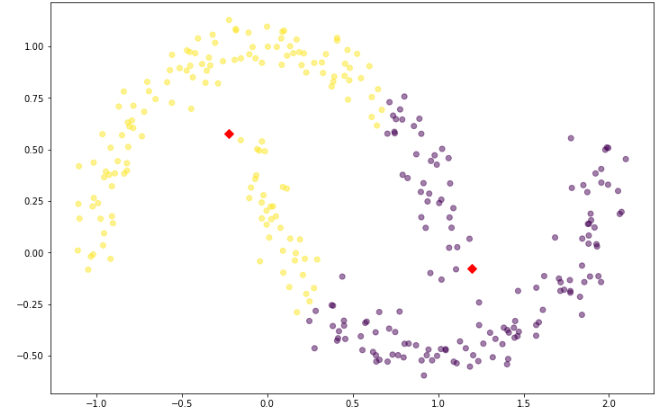
적절한 inertia값을 찾아서 모델링을 해보아도 우리가 기대하는 대로 모델이 생성되지 않는다.
이런 상황을 해결할 수 있는 알고리즘이 DBSCAN이다.
[ DBSCAN ]
DBSCAN은 Density-Based Spatial Clustering of Applications with Noise의 약자로
연쇄적으로 근처의 데이터들을 클러스터 안에 포함시켜 밀도 기반으로 클러스터링을 구현하는 방법이다.
k-means와 다르게 덩어리 형태가 아니어도 문제 해결이 가능한 알고리즘이다.
DBSCAN은 K-means와 구별되는 다음의 특징이 있다.
- K값(클러스터 개수)을 지정해줄 필요가 없다.
- 군집이 형성되지 않으면 이상치로 간주한다.
DBSCAN 절차
- 임의의 한 점으로부터 시작
- 반경 범위내에 최소 포인트 수가 존재하는지 확인
- 최소 포인트 수 이상이 존재한다면 각 포인트들을 중심으로 다시 원을 그어 최소 포인트 수 확인
- 2~3번 반복수행
- 최소 포인트 수 이상 존재하지 않으면, 군집에 포함되지 않은 점으로 이동하여 1~4를 반복수행
- 어느 군집에도 포함되지 않는 점은 이상치로 간주
DBSCAN 알고리즘 사용 시에는 위의 절차에서 언급된 반경 범위와 최소 포인트 수에 대한 하이퍼파라미터를 지정해 주어야 한다.
- epsilon : 반경 범위
- minPoints : 최소 포인트 수
- DBSCAN 모델 만들기 DBSCAN()
# DBSCAN 불러오기
from sklearn.cluster import DBSCAN
# 모델 선언, 학습
model = DBSCAN(eps=0.1, min_samples=3)
model.fit(x)
fitting 한 후에 모델에서 .labels_ 를 통해 찾아낸 군집을 확인 가능하다.
- 1부터 순서대로 군집 번호 부여
- -1은 이상치를 나타냄
clusters = model.labels_
clusters
# array([ 0, 1, 2, 7, 3, 1, 4, 4, 2, 0, 9, 5, 3, 2, 5, 0, 0,
# 6, 6, 0, 3, 4, 2, -1, 2, 0, 2, 2, 7, 8, 5, 2, -1, 2,
# 2, 2, 2, 9, 0, 5, 10, 0, 3, 4, 9, 2, 5, 5, 0, 2, 2,
# 8, 5, 2, 10, 4, -1, 2, 2, 2, 0, -1, 2, 0, 2, 11, 2, 10,
# 5, 2, 0, 2, 2, 0, 4, 2, -1, 2, 6, 2, 0, 4, 8, 5, 2,
# 11, 3, 2, 5, 0, 7, 2, 2, 0, 4, 2, 5, 11, 0, -1, 5, 11,
# 8, 5, 10, 7, 2, 2, 0, 2, 5, 0, 12, 2, 4, 0, 0, 2, 2,
# 12, 6, 4, 0, 0, 2, 5, 2, 2, 5, 8, 6, 8, 2, 2, 0, 2,
# 4, 3, 9, 0, 2, 2, 9, 2, 0, 3, -1, 0, 6, 5, 7, 0, 7,
# -1, 2, 2, 4, 6, 5, 7, 7, 5, 4, 2, 8, 2, 11, 8, 9, 2,
# 5, 2, 9, 1, 0, 7, 0, 0, 2, 9, 7, 0, 8, 6, 7, 5, 9,
# 2, 3, 0, 2, 2, 0, 12, 3, 0, 2, 2, 2, 6, 0, 3, 2, 2,
# 6, 4, 0, 2, 2, 2, 2, 2, 2, 6, 5, 0, 4, 2, 2, 7, -1,
# -1, 0, 8, 2, 6, 0, 5, 2, 0, 0, -1, 0, 5, 2, 0, 4, -1,
# 0, 0, 2, 6, 0, 3, 0, 6, 0, 7, 2, 3, 3, 0, 0, 0, 2,
# 7, 1, 2, 0, 2, 2, 2, 6, 0, 2, -1, 5, 0, 2, 0, 0, 3,
# 5, 2, 2, 0, 2, 0, 3, 3, 0, 7, -1, 2, 2, 5, 5, -1, 9,
# 3, 2, 9, 0, 2, 7, 0, 11, 0, 4, 2], dtype=int64)
위 코드의 결과를 확인해보면 아래와 같다.
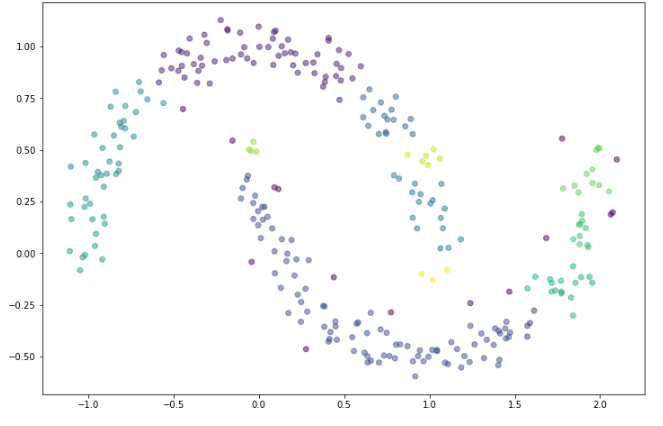
기대했던 것과 다른 결과가 나온 이유는 적절한 파라미터 값을 설정해주지 않았기 때문이다.
모델 선언 함수 DBSCAN()에서 eps=0.2, min_samples=3 으로 옵션을 주고 다시 확인해보면
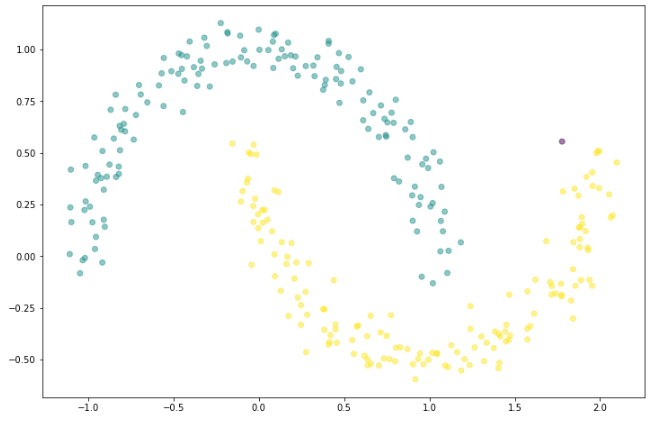
기대했던 모습과 유사한 결과를 얻은 것을 확인해볼 수 있다.
[ 적절한 epsilon 값 구하기 ]
하지만 실제로 사용되는 데이터들을 위와 같이 시각화 해가면서 확인하는 것은 불가능에 가깝다.
때문에 DBSCAN에서도 시각화를 하지 않고도 적절한 하이퍼파라미터 값을 찾을 수 있어야 한다.
이웃 검색을 구현해주는 sklearn의 NearestNeighbors()를 사용해서
각 점과 근처 5개 점과의 평균 거리를 계산하고 그래프를 그려 보았다.
from sklearn.neighbors import NearestNeighbors
knnDist = NearestNeighbors().fit(x)
distances, _ = knnDist.kneighbors(x)
dist = np.mean(distances[:,1:], axis = 1)
dist = np.sort(dist)
plt.figure(figsize = (12,8))
plt.plot(dist)
plt.grid()
plt.show()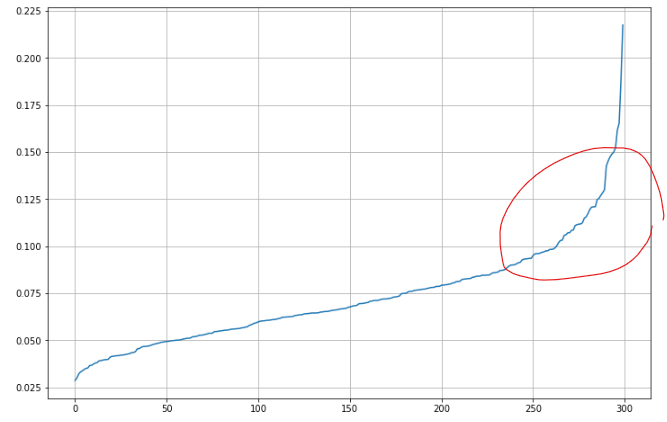
위의 시각화 그래프의 x축은 평균거리, y축은 eps 값을 의미한다.
여기서도 Elbow method를 사용해서 급격히 멀어지기 시작하는 거리 구간을 찾아 eps 값으로 적용해줄 수 있다.
위의 그래프를 참고하여 epsilon=0.125의 값을 주고 다시 모델링 후 시각화해보면
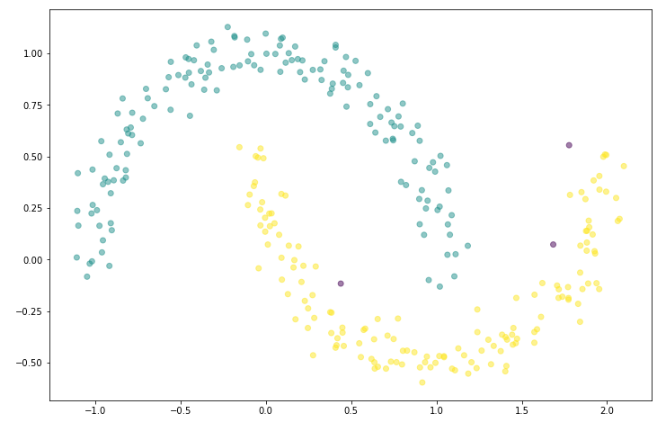
다음과 같이 좋아진 결과를 얻을 수 있다.
K-means와 DBSCAN 등의 모델들로 비지도학습을 하고 나면
그룹을 나누는 것에서 끝나는 것이 아니라 나누어진 그룹들로 의미 있는 결과를 도출해내기 위한 후속 분석 작업이 반드시 필요하다는 것을 알아두자.
'KT AIVLE School' 카테고리의 다른 글
| (7주차 - 22.09.05 ~ 22.09.06) AI모델 해석/평가 (0) | 2022.09.05 |
|---|---|
| (6주차 - 22.08.29) 머신러닝6 - 시계열 분석 (0) | 2022.08.29 |
| (5주차 - 22.08.25) 머신러닝4 - 모델 성능 향상, 앙상블 (0) | 2022.08.26 |
| (5주차 - 22.08.24) 머신러닝3 - 결정트리,SVM,모델성능튜닝 (0) | 2022.08.25 |
| (5주차 - 22.08.23) 머신러닝2 - KNN,로지스틱회귀,분류모델평가 (0) | 2022.08.23 |
