[ 오늘 배운 내용 ]
1. 모델링 개요
2. 선형회귀 (Linear Regression)
- 단순회귀
- 회귀 모델의 평가 방법
- 오차 비 : R-squared
- 오차의 양 : MSE, RMSE, MAE
- 오차의 율 : MAPE
- 다중회귀
교육을 시작하고 드디어 머신러닝 수업이 시작됐다. 그동안 배운 내용 데이터 분석과 데이터 처리는 모델링을 위한 준비작업이었다고 볼 수 있겠다. 주로 데이터를 불러와서 모델을 생성하고 학습시킨 다음 예측을 하는 연습을 코드로 여러번 작성해보았다.
강사님께서 모델링 과정의 코드는 되도록이면 외우라고 하셨는데 오늘 수업을 들으면서 여러 번 직접 입력해보다 보니 손에 익은 것 같다. 코드도 데이터 분석, 처리에 비하면 굉장히 짧은 길이라서 금방 외워졌다.
오늘은 회귀 모델 중에서도 선형 회귀(Linear Regression)를 다루었다. 선형회귀의 단순회귀와 다중회귀 모델을 생성하고 이를 학습시켜보는 연습을 진행했다.
그 다음 R-squared, MSE, RMSE, MAE, MAPE와 같은 회귀 모델을 평가하는 여러 방법들에 대해서 배우고, 단순회귀와 다중회귀 각각의 모델에 대해서 평가를 수행해보았다.
1. 모델링 개요
모델링은 아래의 CRISP-DM 에서의 비즈니스 이해 -> 데이터 이해 -> 데이터 전처리에 이은 모델링(Modeling) 과정에 속한다.
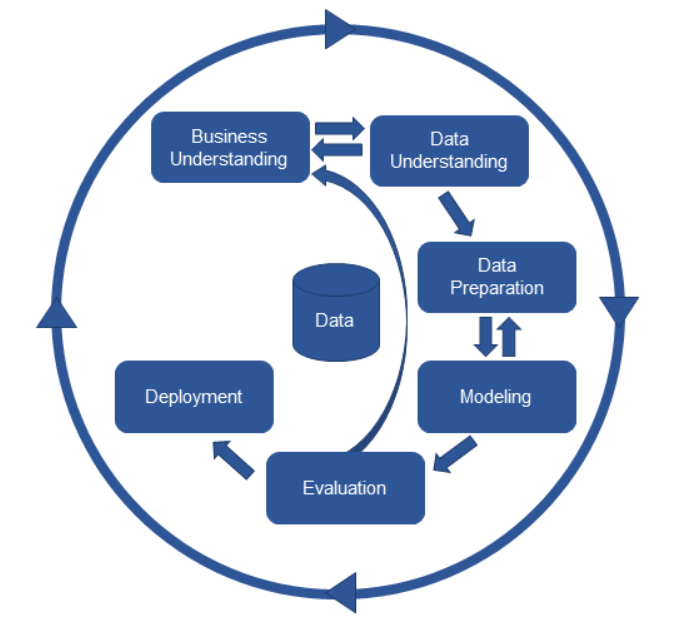
[ 모델링 ]
모델링이란 데이터로부터 패턴을 찾아 오차를 최소화 하면서 y=ax+b와 같은 수학식으로 정리하는 과정이라고 할 수 있다.
패턴이라 함은 x와 y의 관계 안에서 규칙적으로 반복되는 양상을 말하는 것이다.
모델의 목적은 샘플(표본)을 가지고 전체(모집단)을 추정하는 것이다.
패턴을 찾는 방법은 정답이 있는 문제와 정답이 없는 문제에 따라서 나뉘는데 다음과 같이 나눌 수 있다.
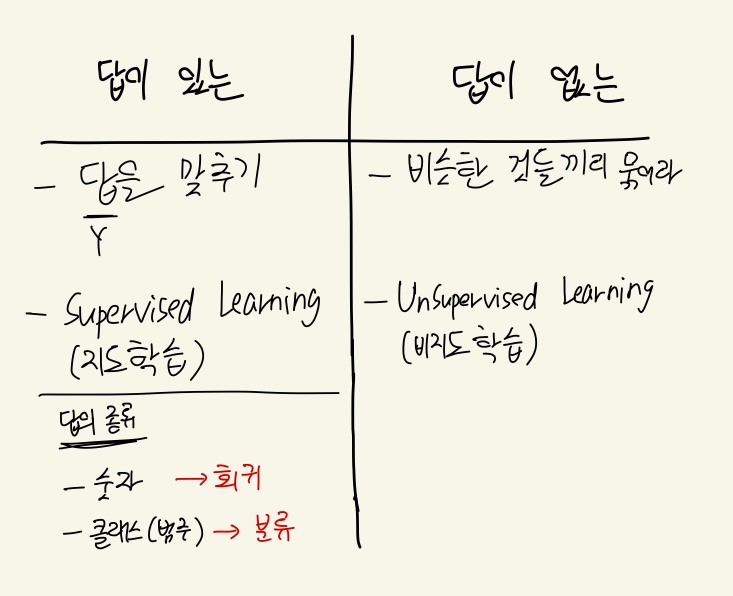
정답이 있는 문제의 경우는 답을 맞추는 것이 목적이다. 컴퓨터에게 답을 알려주면서 패턴을 찾게 하도록 모델을 학습시키는데 이것을 Supervised Learning(지도학습) 이라고 부르며, 문제의 정답이 숫자일 경우에는 회귀(Regression), 답이 클래스, 즉 범주형 일 때는 분류(Classification)라고 한다.
정답이 없는 문제의 경우는 답을 맞추는 것이 아니라 비슷한 것들끼리 묶어주는 것이 목적이며 Unsupervised Learning(비지도 학습)이라고 부른다. 비지도 학습에서는 데이터 안에서 컴퓨터가 알아서 패턴을 찾도록 학습시킨다.
지도학습에서는 문제의 정답의 종류에 따라 회귀와 분류 모델로 나뉜다고 했다.
회귀와 분류의 예시를 보며 구분해보자
회귀(Regression)
- 내일 주가는 얼마일까?
- 이 제품의 다음주 수요량은?
분류(Classification)
- 다음달에 약정기간이 끝나는 고객이 타 통신사로 이동할까?
- 내일 주가는 오를까?
- 더 많은 고객을 끌어들이기 위해서 5000원 쿠폰과 25% 할인 중 무엇이 더 효과적일까?
구체적인 수치로 답을 내야 하는 경우는 회귀, yes/no와 같은 범주로 대답이 가능한 경우는 분류라고 생각할 수 있다.
[ 오차 ]
모델링의 목표는 오차를 최소화 하는 것이다.
모델의 오차는 기본적으로
실제 값 = 모델 + 오차 와 같이 정의할 수 있다. 이를 그림으로 나타내면 다음과 같고 오차를 최소화한다는 말은 모형이 실제를 설명하는(캐치하는) 영역을 최대한 크게 만들어주는 것이다.
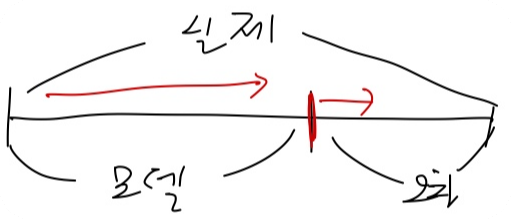
모델링을 수행하기 전 데이터 전처리 단계에서는 데이터를 x와 y로 나눠주고, x와 y를 각각 train과 test용으로 나눠주어야 한다. 모델의 학습과 검증 시에 다른 데이터를 사용해주어야 학습된 모델을 새로운 데이터에 의미 있게 적용하는 것이 가능하다.
train 데이터는 말 그대로 학습에 사용되는 데이터를 말하고, test 데이터는 처음부터 분할한 뒤 모델의 최종완성 후에만 사용하는 최종 테스트 데이터라고 생각하면 된다.
그 밖에 validation 데이터가 있는데 이는 train과 함께 섞었다가 분할했다가를 반복하며 최종 모델을 만드는 과정에서 계속 모델을 만들고 검증하는 용도로 사용되는 데이터이다.
# sklearn : 싸이킷런
from sklearn.model_selection import train_test_split # 데이터 분할
# x와 y로 분할
target = 'Sales'
x = data.drop(target, axis=1) # .drop( , inplace = True)
y = data.loc[:, target] # : 처음부터 끝까지 data['Sales']
# 전체에서 train : test = 7 : 3 으로 나누기
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3) # 테스트쪽 사이즈를 0.3 비율로 지정처음에는 사이킷런의 train_test_split() 메서드를 임포트해주어야 한다.
그다음 데이터프레임을 y와 나머지로 나누어주고, train_test_split 메서드에 위와 같이 인자를 넣어주면 되는데, 반환되는 데이터의 순서는 x_train, x_test, y_train, y_test이기 때문에 꼭 지켜주어야 한다.
test_size 옵션을 통해 학습용과 훈련용 데이터의 비율을 지정해줄 수 있다.
데이터 전처리 과정에서 분할까지 완료하였으니 기본적인 모델링 코드를 익혀보자. 이번 시간에는 선형회귀만 다루었기 때문에 선형회귀를 기준으로 작성하였다.
모델링의 기본적인 순서는 다음과 같다.
- 함수 불러오기
- 모델 선언(설계)
- 학습 (모델링)
- 검증 (예측, 평가)
# 알고리즘 불러오기 : 선형회귀
from sklearn.linear_model import LinearRegression
# 회귀 모델 평가 함수 불러오기
from sklearn.metrics import mean_absolute_error #평균 오차 의미
# 모델 선언 : 알고리즘을 어떻게 사용할지 설정
model = LinearRegression()
# 학습 : .fit ==> 학습은 x와 y의 패턴을 찾아내는 과정
model.fit(x_train, y_train)
# 예측
pred = model.predict(x_test)
# 평가
mean_absolute_error(y_test, pred) # 평균오차(MAE) 사용선형회귀 알고리즘을 사용할 것이기 때문에 sklearn의 linear_model에서 LinearRegression을 임포트 해준다.
그다음에 임포트한 mean_absolute_erorr는 모델 평가에 사용되는 메서드인데 이는 뒤의 모델 평가에서 더 자세히 설명하도록 하겠다.
먼저 임포트한 LinearRegression() 메서드로 모델을 선언해준다.
모델을 선언한 뒤에는 .fit()메서드로 x_train과 y_train에 대해 모델을 학습시켜 주고,
학습시킨 모델로 .predict() 메서드를 이용해 x_test 데이터에 대해 예측을 수행한다.
예측한 결과 pred를 가지고 y_test와 비교해서 모델을 평가한다.
@@위의 기본적인 모델링 코드는 되도록이면 외우자@@
2. 선형회귀 (Linear Regression)
선형 회귀는 단순회귀와 다중회귀로 나눌 수 있다.
- 단순회귀 : 하나의 예측변수로 하나의 결과변수를 예측
- 다중회귀 : 복수의 예측변수로 하나의 결과변수를 예측
y = -2x + b 와 같은 모양의 직선식이 나오면 단순회귀
y = -2x1 -1.5x2 + 3x3 + b 와 같은 모양의 평면식이 나오면 다중회귀 라고 할 수 있다.
선형회귀는 데이터를 하나의 직선으로 요약해준다. 선형회귀식(직선, 평면...)으로 Target과의 관계를 설명해준다.
하지만 자료를 설명하는 직선은 여러 개가 될 수 있기 때문에 그 중 가장 데이터를 잘 설명하는(전체 오차가 가장 적은) 직선 한 개를 선정하는 방법이 필요한데 머신러닝에서는 주로 오차를 조금씩 줄여가며 반복적으로 직선을 찾는 최적화를 사용한다.
최적화 작업은 위에서 작성해본 모델링 코드의 .fit() 메서드가 수행해준다.
.fit() 메서드에서는 feature들과 target과의 관계, 패턴을 선형회귀 알고리즘을 이용하여 모델(함수)로 만들어준다.
[ 단순회귀 ]
먼저 하나의 예측변수로 하나의 결과변수를 예측하는 단순회귀 모델을 구현 해보았다.
데이터는 보스턴 집값 데이터를 사용했고, lstat(하위계층 비율)로만 집값(medv)을 예측하는 모델을 만들어 보았다.
# 학습에 사용할 변수 지정
features = ['lstat']
# 지정된 변수로 데이터셋을 만들기. (x는 2차원 이어야 한다. -> 데이터프레임)
x_train1 = x_train[features]
x_val1 = x_val[features]
# 모델링용
from sklearn.linear_model import LinearRegression
# 회귀모델 평가용
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error, mean_absolute_percentage_error
model1 = LinearRegression() # 모델선언
model1.fit(x_train1, y_train) # 모델링(학습)
pred1 = model1.predict(x_val1) # 검증(예측)
mean_absolute_error(y_val , pred1 ) # 검증(평가)
# 4.138380487348265모델링에 사용되는 x는 2차원이어야 하기 때문에 시리즈가 아닌 데이터프레임으로 넘겨주기 위해 ['lstat']로 지정해준다.
모델을 불러오고 선언, 학습, 예측해준 뒤 예측값과 실제 값을 비교해서 검증해주었다.
여기서 만들어진 모델의 내부를 열어보자.
생성된 회귀모델을 함수 형태로 볼 때 (y = w1x1 + w0) w1에 해당하는 부분이 회귀계수(기울기), w0에 해당하는 부분은 y절편이다. 이러한w0, w1 등의 값들을 가중치(weight) 혹은 파라미터 라고 부르며, 이 값들은 다음의 코드로 확인 가능하다.
- 회귀계수 : 모델.coef_
- Y절편 : 모델.intercept_
print('회귀계수 : ', model1.coef_)
print('절편 : ', model1.intercept_)
# 회귀계수 : [-0.9568563]
# 절편 : 34.676249051494665모델의 회귀계수와 Y절편을 통해 다음과 같은 lstat와 medv의 단순회귀모형 직선식을 얻어낼 수 있다.
y = -1 x lstat + 35 (반올림함)
모델의 식을 얻어냈으면 모델을 통해 비즈니스 의미를 찾아내는 것이 중요하다.
medv(집값)의 단위는 1000달러이고, lstat(하위계층비율)의 단위는 %이다.
- 회귀계수 -1의 비스니스 의미
- 하위계층의 비율이 1% 올라가면, 집값은 1000달러 하락
- Y절편 +35의 비즈니스 의미
- 하위계층의 비율이 어떤지에 상관없이 집값, 하위계층이 없을 때의 집값 등 ... (오차와 헷갈리지 말것)
이런 식으로 얻어낸 모델을 비즈니스 의미로 해석할 수 있어야 한다.
[ 회귀 모델의 평가 방법 ]
회귀 모델은 두가지 관점으로 평가를 한다.
- [y의 평균] 모델의 오차 vs [회귀] 모델의 오차
- 실제 값(y) vs 회귀 모델의 예측값
y의 평균모델의 오차와 회귀모델의 오차를 비교하는 경우는 오차의 비, 설명력, 결정계수 등의 지표로 평가가 가능하고 R^2 Score 방법을 사용한다. (y의 평균모델은 y의 평균을 말한다. 평균은 통계학에서 사용되는 가장 단순한 모형 중 하나)
실제 값과 회귀 모델의 예측값을 비교하는 경우는 오차의 크기, 오차율 등의 지표로 평가가 가능하고 MSE, RMSE, MAE, MAPE 등의 방법을 사용한다.
[ 오차의 비로 평가하기 : R-squared (R^2)]
R-squared는 평균 모델의 오차와 회귀모델의 오차를 비교했을 때, 평균 모델의 오차 대비 회귀모델이 해결한 오차의 비율을 말한다. 즉, 회귀모델이 얼마나 오차를 해결(설명)했는지를 나타내고, 결정계수, 설명력 이라고 부르기도 한다.
정말 간단하게 말해서 평균 대비 얼마나 좋아졌는지를 확인해보는 것이다.
R^2 score는 다음의 3가지 지표를 활용해서 구해준다.
- 평균 모델과 실제 값과의 차이 (SST)
- 평균 모델과 회귀모델과의 차이 (SSR)
- 실제 값과 회귀모델과의 차이 (SSE)
R^2는 평균모델로 예측한 원래 모델의 오차를 얼마나 해결했는지를 나타내는 것이기 때문에
SSR/SST 로 나타낼 수 있는데, 실제 사용 메서드에서는 1 - ( SSE/SST )로 계산된다.
코드로 작성할 때는 다음과 같이 r2_score( 실제값, 예측값 ) 으로 평가해준다.
from sklearn.metrics import r2_score
r2_score(y_val, pred1)
# 0.6315401111275217r2_score 값은 얼마나 오차를 해결했는지를 나타내기 때문에 클수록 좋다고 볼 수 있다.
[ 오차의 양과 율로 평가하기 : MSE, RMSE, MAE, MAPE ]
회귀모델을 오차의 양과 율로 평가하는 데에는 다음과 같은 방법들이 존재한다.
- 오차의 양 : MSE, RMSE, MAE
- 오차의 율 : MAPE

위와 같이 정리가 가능하다. y는 실제 값, y^는 예측값을 말한다.
Mean Squared Error (MSE) 는 오차제곱의 평균 이라고 할 수 있으며, 실제값과 예측값의 제곱오차의 평균을 구한 값이다.
MSE에 루트를 씌워준 값은 Root Mean Squared Error (RMSE) 라고 하며 MSE와 RMSE는 +와 -를 +로 바꿔주고, 큰 값은 더 크게, 작은 값은 더 작게(0~1사이의 수) 만들어준다는 특징이 있기 때문에 튀는 오차를 확인하기 좋은 방법이다.
Mean Absolute Error (MAE)는 평균오차라고 하며 실제값과 예측값의 오차의 절대값의 평균을 구한 값이다.
실제값과 예측값의 오차를 실제값으로 나눈 오차율의 평균을 구해준 값은 Mean Absolute Percentage Error (MAPE) 라고 하며 실제값 대비 오차의 비율을 확인해볼 수 있다.
위의 평가방식들을 코드로 작성하여 확인해보았다.
# 회귀모델 평가용
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error, mean_absolute_percentage_error
# MSE (오차제곱의 평균)
mean_squared_error( y_val , pred1 )
# 31.563327757446412
# RMSE (오차제곱의 평균 -> 루트씌워줌)
mean_squared_error( y_val , pred1 , squared = False) # squared=False로 지정하면 MSE에 루트를 씌운 것과 같음 ==> RMSE
# 5.618124932523877
# MAE (평균오차)
mean_absolute_error(y_val , pred1 )
# 4.138380487348265
# MAPE (평균오차율) : 원래 개념은 100(%)을 곱해햐 한다. 그렇지만 sklearn 함수는 100을 안 곱한 채로 결과를 준다.
mean_absolute_percentage_error(y_val , pred1 )
# 0.22398686231166276- MSE : mean_squared_error( 실제값, 예측값 )
- RMSE : mean_squared_error( 실제값, 예측값 , squared = False )
- MAE : mean_absolute_error(실제값, 예측값 )
- MAPE : mean_absolute_percentage_error( 실제값,예측값 )
RMSE의 경우에는 메서드가 따로 있는게 아니고 mean_squared_error에 squared=False 옵션을 주어서 제곱을 하지 않게 하여 구해준다.
모두 오차를 나타내는 값들이기 때문에 작은 값일수록 좋다고 볼 수 있다.
주로 사용되는 방법으로는 RMSE, MAE, MAPE가 있다.
[ 다중회귀 ]
복수의 예측변수로 하나의 결과변수를 예측하는 다중회귀 모델을 만들어 보자.
다중회귀모델에서는 feature가 2개 이상이고, feature들 간에 독립성을 가정하고 모델을 생성해야 한다. feature들 간에 독립성이 있다는 것은 feature들이 서로 관계가 없다는 것을 말한다.
feature들 간에 독립성을 가정해야 하는 이유는 다중 공산성 때문인데, 다중 공산성이란 하나의 독립변수가 다른 여러 개의 독립변수들로 잘 예측되는 경우를 말한다.
다중 공산성이 있으면 개수 추정이 잘 되지 않거나 불안정해져서 데이터가 약간만 바뀌어도 추정치가 크게 달라진다. 때문에 계수가 통계적으로 유의미하지 않은 것처럼 실제와 많이 다른 결과가 나올 수 있다.
데이터는 보스턴 집값 데이터를 사용했고, lstat(하위계층 비율)과 ptratio(학생/교사 비율)로 집값(medv)을 예측하는 모델을 만들어 보았다.
# 학습에 사용할 변수 지정
features = ['lstat', 'ptratio']
x_train4 = x_train[features]
x_val4 = x_val[features]
# 모델 만들기, 학습, 예측
model4 = LinearRegression()
model4.fit(x_train4, y_train)
pred4 = model4.predict(x_val4)
# 회귀계수 확인
print(list(x_train4))
print(model4.coef_, model4.intercept_)
# ['lstat', 'ptratio']
# [-0.82877003 -1.25776375] 56.231763304678594만든 모델의 회귀계수를 바탕으로 선형회귀식을 적어보면
medv = -0.83 x lstat -1.26 x ptratio + 56 와 같은 식을 얻을 수 있다.
위에서 만들었던 단순회귀 모형의 lstat와 medv의 선형회귀식과 회귀계수가 달라진 것을 알 수 있다.
다중회귀식으로 얻어낸 선형회귀식에서 각 feature들의 회귀계수를 보기만 해서 어떤 feature가 더 중요하다고 판단할 수는 없다. 이는 feature들 간의 범위(단위)가 달라서 같은 숫자값이어도 feature별로 서로 다른 의미를 갖고 있을 수 있기 때문이다.
따라서 Scaling을 통해 변수들의 범위를 맞춰줄 필요가 있다.
'KT AIVLE School' 카테고리의 다른 글
| (5주차 - 22.08.24) 머신러닝3 - 결정트리,SVM,모델성능튜닝 (0) | 2022.08.25 |
|---|---|
| (5주차 - 22.08.23) 머신러닝2 - KNN,로지스틱회귀,분류모델평가 (0) | 2022.08.23 |
| (4주차 - 22.08.16~22.08.19) 미니프로젝트1 (0) | 2022.08.22 |
| (3주차 - 22.08.12) 데이터 분석 및 의미 찾기 3 - 이변량분석2 (2) | 2022.08.15 |
| (3주차 - 22.08.11) 데이터 분석 및 의미 찾기 2 - Seaborn,이변량분석1 (0) | 2022.08.12 |
